Pentominoes
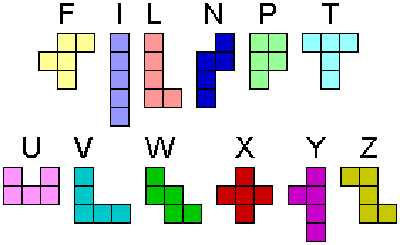
Pentominoes are shapes made from five joined squares. Joined with at least one common side. There are twelve ways to create these shapes. They have been named T, U, V, W, X, Y, Z, F, I, L, P, and N respectively.
Two restriction to what counts as a pentomino.
- If a shape can be rotated to look like another, the two shapes are the same.
- If a shape can be flipped to look like another, the two shapes are the same.
As a mnemonic device, to remember the names, is the letters from the end of the alphabet (TUVWXYZ) and the word FLIPN.
History:
Pentominoes are said to have been "invented" by Solomon W. Golomb in 1953 when he gave a talk to the Harvard Mathematics Club.
While he was the first to use the name, pentominoes, the idea of five squares and how they might be arranged has been around since a much earlier time.
The earliest reference to a puzzle of this sort appears to be in The Canterbury Puzzles, by Henry Dudeney, published in 1907. The idea is so obvious that it may have been known to many people independently.
Puzzle making all twelve pentomine puzzles:
Give the students a sheet of graph paper and challenge them to find all the ways five squares can be arranged (12) to make a shape.
Alternative - Box pattern challenge
Show students the X shape and show them how it can be folded into a box ( without a lid).
Challenge them to find all the different patterns that can be used to make a box (8).
Puzzle rectangles using all pentominoes each with an area of 60 squares (5x12).
Pentominoes can be assembled into four different rectangle puzzles -
- 3 x 20, ( 2 solutions)
- 4 x 15, ( 368 solutions)
- 5 x 12, ( 1 010 solutions) and
- 6 x 10 (2 339 solutions).
Solution sources:
The first investigation of these puzzles by computer was probably by Dana Scott in 1958. The results were summarized in an article by C. J. Bouwkamp in the Journal of Combinatorial Theory in 1969. and The Puzzling World of Polyhedral Dissections, Chapter 2 - Two-Dimensional Combinatorial Puzzles, by Stewart T. Coffin
With 2,339 solutions, you might expect finding one would be quite easy. If so, you are due for a surprise!
Other puzzles:
Create rectangles with areas of: 35, 45, 55, 65, 85, 125,
Create a cross with all 60 squares that is 9 wide, 14 high, and 3 wide at its narrowest.
One 6x10 solution:
