Arguments, Reasoning, Logic, & Proof
Arguments, Reasoning, Logic, and Proof
Development of valid arguments, reasoning, logic, & proof
- Introduction
- Truth, reality, & relativism
- Information as changing
- Definitions
- Argument
- Reasoning
- Proof
- Logic
- Argument
- Proof
- types of proof
- Proof as common sense
- Mathematical proof
- Visual representation as proof,
- Comparison of properties as proof with sufficient & necessary for equivalent properties & exclusion of independent properties - foundation of reasoning & proof
- Proof by disproving with a counterexample,
- Deductive proof,
- Proof by analogy or metaphor
- Proof by exhaustion or identification, or elimination
- Logical reasoning
- Logical reasoning errors
- Mathematical examples for reasoning and proof
- Teaching suggestions related to proof
- Misconceptions and fallacies of inaccurate proofs
- Scoring guide
- Summary
Introduction
Argument, reasoning, logic, and proof are ways we make sense of the world. Whether it is by ourself or with others, we strive to better understand the world, to satisfy our curiosity to know and understand, to survive, and to create a good life.
To achieve this we observe, identify information to think about and attempt to make sense of our perceptions by discovering verifiable repeatable patterns. As our understanding grows, we are excited to share our new understandings with others. In the process of sharing, others may accept, reject, alter, and bring other ideas to create their understanding of the world for a better life.
Together people share their ideas to make decisions on how to deal with any differences. Within our biological ways of learning, they chose ways to validate their acceptance or rejection of ideas. Some of their choices include:
- The use or rejection of facts, concepts, & generalizations
- Use propaganda to promote a particular point of view
- Critical thinking
- Problem solving
- Science inquiry for explanations & understanding
- Decision making
- Cooperation skills
- Problem solving, reasoning, & proof vocabulary K - 6
- Development of logical reasoning
- Cognitive development of reasoning and supporting tasks. activities, & explanations
- Misconceptions & transductive reasoning
- Bias & propoganda
- Perception, illusions, visualization, memory, learning, and development
As people consider different information they must decide how to agree on what they will accept as their common knowledge (truth) and understanding. And over the years modern cultures have repeatedly turned to the use of arguments, reasoning, logic, and proof to establish their cultural knowledge and legal systems.
This article focuses on argument, reasoning, logic, proof and related information. First, we start with a few philosophical ideas about truth, relativism, and information. Then definitions of argument, reasoning, logic, and proof. Followed by examples of what each is, how to use them, and some instructional suggestions.
Truth, reality, & relativism
Truth is that which agrees with fact and reality.
Reality is the state of things as they actually exist as opposed to a belief or idealistic interpretation of them.
Relativism is the belief that knowledge, truth, and morality exist in relation to culture, society, or historical context, and are not absolute.
Problems arise when people have different ideas of what is real and factual and how to construct what is moral and apply it socially.
Problems and reasoning
People generally want to be empowered with choice and will extend the idea of relativism to claim each person can have their own individual reality to validate choice and to avoid confrontation.
However, while this usually works in situations like food and clothing choices, it fails in situations where personal choice interferes with another's personal choice.
If we take a relativist position for all knowledge and truth and accept anyone’s view as legitimate, claiming there is no established truth, that will make all personal truths and alternative facts justified, which can be good or bad. Good if people are open-minded enough for peaceful resolution of differences. Bad if, it leads to conflict and violence with no path to cooperate to establish collective principles and procedures to work together for a common purpose and progress.
Historical rejection of relativism
Protagoras, argued that each person has their own reality and it should be accepted as truth. Plato rejected this relativism based on the claim that if each person can determine reality, then everyone is infallible and whatever every person determines as truth, is true. He goes on to explain this is a false logic, because if a person thinks relativism is false, then that would be true. Therefore, if relativism is true, it must be false. A contradiction, as it can't be both true and false at the same time. Source
Information as unchanging
Recognizing knowledge that is constantly changing doesn’t make it useless or illegitimate.
Definitions
Argument is a reason or set of reasons with the aim of persuading others that an action or idea is right or wrong.
Reasoning is the action of thinking about something in a logical, sensible way.
Reasoning with logic includes:
- Assumption or premise
- Reasoning, inferences, evidence, and warrants used to get
- Conclusions
Reasoning, without logic, is an innate non-verbal action to make inferences about consequences.
Proof is an explanation accepted by a community at a given time. The rigor of the proof is dependent on the members of the community. Communities can range from a kindergarten class as a community where proof is relative to what a particular child thinks; to a community of mathematicians, who require a formal logical proof.
Logic is the procedure used to tell the difference between good reasoning and bad reasoning by discovering inaccurate information.
People do not always reason according to standard logic. They will often agree with something, but what they agree with does not follow logically from their given premises; and they will also often reject logical conclusions and not agree.
Argument
Argument is a reason or set of reasons with the aim of persuading others that an action or idea is right or wrong or as an explanation of results or consequences in certain situations.
Other definitions & related ideas
Argument is an independent variable associated with a function and determines the value of that function.
Argument is more specific than a proof.
While one definition of argument is an exchange of diverging or opposite views, which can be a fight. However, an argument with relation to reasoning and proof, is not a quarrel or dispute.
Argument & proof difference. As nouns the difference between argument and proof, is that argument is a fact or statement or reason used to support a claim or proposition, while proof is an effort, process, or operation designed to establish or discover a fact or truth, an act of testing, a test, a trial, conclusion, or consequence.
Examples
Argument with a premise, evidence, and a conclusion.
- Premise - All vegetables (A) are plants (B).
- Evidence - Beans (C) are vegetables (A).
- Conclusion - Beans (C) are plants (B).
Example with attributes that may be necessary but not sufficient.
- Premise - All dogs (A) have hair (B).
- Evidence - This animal (C) has hair (B).
- Conclusion - This animal (C) is a dog (A).
Examples with attributes that may not be sufficient or use selective instances.
- We had a record snowfall, therefore, it proves global warming can’t be happening.
- This is the warmest summer on record, therefore, it proves global warming is happening.
Examples where the premise isn’t true.
- All smart people have a college degree.
- I don’t have a college degree.
- Therefore, I am not smart.
Example where the conclusion isn’t true.
- If you have a college degree, you are smart.
- I don’t have a college degree.
- Therefore, I am not smart
Example where the premise is an inaccurate exaggeration.
- I always fail a test
- I have a test tomorrow.
- Therefore, I will fail.
Suggestions to examine arguments:
- Is the premise true?
- Is the evidence accurate? Is it sufficient or only necessary? What is it’s source?
- Is the conclusion logical?
- Is it based on inaccurate language, perception, memory, facts, biases, emotions, influences, culture differences?
Proof
Proof is an explanation accepted by a community at a given time. The rigor of the proof is dependent on the members of the community. Communities can range from a kindergarten class as a community where proof is relative to what a particular child thinks; to a community of mathematicians, who require a formal logical proof and proof in a court of law beyond a reasonable doubt.
Types of proof
Proof as common sense
Proof is the essence of mathematics. It is what makes mathematics valid. The making of conjectures about the use of mathematics and the justification of conjectures as solutions. Anything less can not present the true nature of mathematics. Education must empower learners to make conjectures, create solutions, and justify the methods for attaining the results; instead of focusing on justifying their use of steps from teacher taught procedures.
While mathematical proof validates some kinds of conjectures as solutions, not all questions, problems, or investigations require a formal logical proof. Other ways of making decisions or justifying them can also be useful and appropriate in different situations.
Mathematical proof
Mathematical proof is any sound, convincing, and unquestionable explanation, for anyone who understands the concepts, and for which no counterexample can be given. It can be provided for explanation, communication, verification, systematization, and discovery. See examples
Visual representation as proof
Visual comparison is the first kind of proof offered to and demonstrated by children.
- Look! Is it a dog?
- Is it a circle?
- Is it a triangle?
- It's a square see.
Young children look at an object and compare it to their mental visual representations. If it looks like one of their previous minds-eye views, that is proof enough. They do not use properties as justification. It is a holistic visual comparison.
Comparison of properties as proof by reasoning with necessary & sufficient
Also - foundation for reasoning & proof
The identification and use of properties appear as children begin to take closer looks at objects, images, or visual images. They begin to compare properties or characteristics of the objects along with visual representations.
For example, different and similar properties of dogs, cats, cow, pigs, squares, triangles, and other objects are added to their mental images. Images of dogs with four legs. Dogs with fur. Dogs that bark. The number of sides on squares, triangles, and circles. How the sides are curved or straight.
The mapping of properties from a person's mental representation of an object to a questionable object is an example of comparison being used as evidence to create a proof of equivalence or not. This use of matching properties or mapping properties from one to another to use as evidence to build a proof is rarely used by children. Children and even adults persist on using observations. If it looks like a cat, then it is a cat.
Teachers' attempts to teach children to use scientific classification as a way to identify living organisms often results with the learner's persistent claims that dolphins and whales are fish, snakes don't have bones, and humans aren't animals.
However, with continued experiences of having learners identify properties, classify by properties, and organizing solutions based on properties, they will increasing use this as a strategy of proof.
In geometry, for example, learners can be asked to identify properties and use those properties to identify and organize figures and shapes by their properties. With these kinds of experiences we learn that some properties are necessary for an object to belong to a group and others are not.
We also learn there are properties that are independent of the conditions they are exploring. We learn there is a sufficient number of properties needed to describe or identify a particular object or group of objects. And we learn that if two objects have the same necessary and sufficient properties, then they are equivalent.
Stated another way:
To prove one object as a member of a class or congruent with another object, then all of the necessary and sufficient properties of the object, class, or group must be identified for the questionable object.
Summary
When you use the ideas of sufficient, necessary, equivalent, and independent conditions, you have the tools for reasoning and proof.
Independent conditions are properties or conditions that vary independently of the other.
Example size and shape. It is possible for the shape of a square to have an infinite variety of sizes and still have the shape of a square. Similarly the properties necessary to make a shape a square, do not include size. Size is an independent condition of being a square.
Examples:
1 - Triangle
Lets explore these ideas for the class of objects known as triangles. What are the necessary conditions for a triangle?
Necessary properties/conditions/characteristics of a triangle
- Plane figure
- Closed figure
- Three sides
- All sides are straight lines
Not Necessary properties/conditions/characteristics of a triangle
- Three dimensions figure
- Open figure
- Four sides
- One side or more has a curve
Which of the following necessary conditions must be included for all the sufficient conditions needed to describe a triangle or for a figure to have to be a triangle?
- A plane figure - Not sufficient, because there are plane figures that are not triangles
- A closed figure - Not sufficient, because there are closed figures that are not triangles
- Three sides - Not sufficient, because there are figures with three sides that are not triangles. In fact all polygons have three sides and more
- All sides are straight lines - Not sufficient, because there are other shapes with all sides being straight lines.
Summary question to ask
- Does this list include sufficient conditions or all the minimum number of necessary conditions to represent a triangle?
The list is sufficient And all are necessary for a plane figure to be a triangle or for the list to be used to define a triangle.
Summary
These ideas can be used for comparison and to categorize or group objects by their common properties.
Or when considering if two things are equivalent or congruent. Triangles with identical necessary and sufficient properties are congruent.
2 - Equivalent sets of numbers
Example for a proof of equivalent descriptions of numbers.
Two sets of properties that represent a whole number.
- Set one - It is greater than one, it is less than three, it is a whole number. [2]
- Set two - It is the smallest positive whole number that is also an even number. [2]
To prove these are equivalent conditions we must show they are both necessary and sufficient.
They are, as they lead to the same conclusions.
This makes it possible to write:
- the whole number greater than one and less than three is equal to the smallest positive even whole number.
- Further it would also be valid to set both equal to 2.
Summary for comparison of properties as proof with necessary & sufficient
Take your time and make this information YOURS.
If you do, then you can use it to create questions to probe other learners' depth of understanding. By having them consider:
- What is necessary?
- What is sufficient? And
- Is there something more that needs to be added to make something sufficient?
- Is there something included that is not necessary?
- What statements or groups of statements are equal or equivalent?
- What does it look and sound like if we put them together as equals?
Proof by disproving with a counterexample
We make a conjecture and find an example that doesn't fit the conjecture, then can claim we have disproved the conjecture by discovering a counterexample.
Example 1
- Conjecture - The squares of all numbers are odd.
- Example - Three squared is nine.
- Counterexample - Two squared is four.
Example 2
- Conjecture - The squares of all numbers are even.
- Example - Two squared is four.
- Counterexample - Three squared is nine.
Deductive proof
Deductive proof - uses a general definition to include a specific instance or a premise to reach a conclusion. Is generalizable to all instances with the same characteristics that satisfies the givens or represents the given class, definition, or law.
Example
Start with a set of assumptions and use them to derive a valid conclusion.
Assumptions
- It is a whole number
- It is a perfect square
- It is between 40 and 100
- It has a factor of three
What is it?
Specific instances
- Whole numbers are 1, 2, 3, 4, ..
- Perfect squares are 2, 4, 9, 16, 25, 36, 49, 64, 81, 100 ...
- Whole number perfect squares, between 40 and 100 are 49, 64, 81
Conclusion - The only one number of 49, 64, and 81 to have a factor of three is 81.
More examples in logical reasoning - deductive reasoning
Proof by analogy or metaphor
Proof by analogy or metaphor - mathematicians might distinguish analogies as a directly related comparison of two like arguments and metaphor as indirectly related.
Analogies:
- Feathers are to birds as scales are to fish
- Feathers are like scales (body coverings) and birds are like fish (animals).
- Feathers : bird :: scales : fish :: hair : mammals
- Den:fox :: hive:bees
- Bird :: nest:: burrow:rabbit
The relationships are obviously clearly definable relations of the respective parts or artifacts to animals as well as parts or artifacts to parts or artifacts and animals to animals.
Metaphors are not as tight - At night all cats are black. Can not substitute - like the previous analogies. There is a violation of syntactic structure. Night relates to black as light or dark and black relates to cats as to color - white, brown, yellow, black; while the figurative meaning of the metaphor is something unrelated.
Examples
Proof of the Commutative Property
To show students a specific example, can be a starting point of a proof. Specially for very young children. Like 3 + 5 = 5 + 3; can be demonstrated by gluing three beans to card stock and five beans to card stalk, then showing that either order of the cards has a cardinality of eight beans. However, if we stop here we must recognize it is not a proof. In fact it is recognized as not being a proof - by attempting to prove a specific example or a selective instance as equivalent for all possible examples.
To make it a proof the idea must be generalized for all possible cases or the infinite number of cases that might exist. This can be suggested by asking what happens if the number of beans are increased. Again, young children usually reach a limit because of their limited understanding of the number system. However, as students understanding of number systems increase toward a conceptualization of infinity, the generalization can be pushed toward infinite possibilities and the equivalence for all of them. For children to be able to do this they will need to have achieved all the conditions for conservation. When you believe this is so, the next example can be presented.
Prove that when you add any two numbers the sum will be the same no matter the order of the numbers. While all the students may be convinced of this it is necessary to push them to explain why it would work for addition of all numbers (infinity again) for the case of whole numbers. Have them create an explanation that they could give to another person (art, music, PE. teacher or principal).
To move to infinity students should be able to show with manipulatives and a drawing that represents additional or less numbers. You can question by asking for repeated larger or smaller numbers.
Proof by Exhaustion or identification or exhaustion
Identify all examples and justify their inclusion, as members of a solution, and reasons for their inclusion. Along with the elimination of all elements among the set of possibilities that are not solutions. See card trick for an example.
Logical Reasoning
Let's combine logic and reasoning for logical reasoning. Reasoning with accurate information to attain accurate conclusions, inferences, or outcomes. Deductive reasoning, inductive reasoning, and inferential reasoning are examples.
Logical reasoning includes:
- Assumption or premise
- Reasoning, inferences, evidence, and warrants used to get
- Conclusions
In if-then reasoning, the if part is the premise (what we are arguing for or against) and the then part is the conclusion. The whole statement is the argument.
Deductive reasoning
Four Logical General statements with examples
- Proposition: If you do X, then you may do Y.
- Inverse: If you do NOT do X, then you may NOT do Y.
- Converse: If you do Y then you do X.
- Contrapositive: If you do NOT do Y then you will NOT do X.
Specific examples
- Proposition: If there is rain, then there are clouds.
- Inverse: If there isn't rain, then there aren't clouds.
- Converse: If there are clouds, then there is rain.
- Contrapositive: If there aren't clouds, then there isn't rain.
Statements equivalent to a proposition
Proposition: If there is rain, then there are clouds.
- Rain implies there are clouds.
- If there is rain, then there are clouds.
- There is rain only if there are clouds.
- There are clouds if rain.
- If there are no clouds, then there is no rain.
- Rain is sufficient for clouds.
- Clouds are necessary for rain.
Statements not equivalent to the proposition:
Proposition: If there is rain, then there are clouds.
- If there are clouds, then there is rain.
- If there isn't rain, then there aren't clouds.
- There are clouds only if there is rain.
Statements coded:
- Proposition: If X, then Y.
- Inverse: If ¬ X, then ¬ Y.
- Converse: If Y, then X.
- Contrapositive: If ¬ Y, then ¬ X.
Equivalent statements:
X ⇒ Y
if X, then Y
X only if Y
Y if X
¬ Y ⇒ ¬ X
X is sufficient for Y
Y is necessary for X
Examples - Label each of the following statements from the proposition and tell which is true if the proposition is true.
Proposition: If John has work to do, then he is in his seat.
If John doesn't have work, then he isn't in his seat.
If John is in his seat, then he has work to do.
If John isn't in his seat, then he doesn't have work to do.
Label each of the following statements from the proposition and tell which is true if the proposition is true.
Proposition: If Mary doesn't do her work, then she will not go to recess.
If Mary does her work, then she will go to recess.
If Mary will not go to recess, then she did not do her work.
If Mary goes to recess, then she did her work.
Write four of your own.
Sample problems
1. Marty asked her teacher if she should do a report. The teacher said, "Marty, you can earn an A only if you do the report." Marty did the report, but did not get an A. Did the teacher lie?
2. A teacher told Jim that if he didn't do his work he wouldn't go outside to recess. Jim didn't do his work and the teacher let him go to recess. Did the teacher lie?
More examples
Assume that the first statement is true, tell if the following statements are true, false, or questionable.
If you wear nice clothes to school, then your teachers will be impressed.
- If your teachers will be impressed, then you wear nice clothes to school.
- If your teachers won't be impressed, then you don't wear nice clothes to school.
- If you don't wear nice clothes to school, then your teachers won't be impressed.
For the statements, above this time assume the first statement is false, now tell if the same three statements are true, false, or questionable.
Inductive reasoning
Inductive reasoning - is using the specific to create the general or conclusion. Rolling two die hundreds of times to find the probability of the different sums. Inductive reasoning is the step child of deductive reasoning since it is based on experiment and variables. For example - statistical reasoning is not accepted in a courtroom.
See math and probability
Common errors in logical reasoning:
Circular reasoning:
James: "Grass is green."
Lynn: "Why do you think so?"
James: "Because it is green."
Proof by selected instances:
John has never seen his parents fight. He thinks that all married couples never fight.
Proof by failure to find a counter example:
Mary has never seen a purple elephant, therefore they do not exist.
Proof by counter example:
You are never on time. What do you mean? I was yesterday.
Avoiding the question:
Is it bad doc? It's too early to say.
Special pleading:
Dad: "Slow down your going 60 mph and that's over the speed limit."
Son: "You drive 65 mph".
Dad: "That's different. I know what I'm doing."
Faking a connection:
A dog is an animal. A cat is an animal. Therefore a dog is a cat.
Don't forget substituting the converse or inverse for the proposition.
Sample problems
Directions
Tell if the following are logical or not and what kind of faulty reasoning is being used, if they are faulty.
1. It doesn't make any difference to me whether you believe me or not, because I don't care one way or another whether or not you believe me.
2. Development of solid foundations of reasoning is essential to the proper education of a person. Therefore, if someone is to be educated properly, then she must at least acquire a thorough knowledge of the basics of reasoning.
3. "Dad, can I use the car tonight?"
"What do you think?"
"Nope. You told me not till next week."
4. I know that I can not learn a foreign language, because when I took Spanish I received an F.
5. My mother can cook anything. She is always trying new recipes and they always turn out great.
6. Daughter: "Why won't you let me go downtown? You said you did when you were my age.
Mother: "That's different. The times have changed, the size of the town, and the ways of the people."
7. John must be a very good person, because I have never heard anything bad about him.
8. "Sara, will you go out with me tonight?"
"Get lost."
9. All teachers are important people. You are a teacher. Therefore, you are an important person.
10. "Mom, Why is the sky blue?"
"Ask your dad."
11. "Mom, why is the sky blue?"
"because red wouldn't look so good."
12. "Mom why is the sky blue?"
"I don't know."
13. All traditional teachers favor corporal punishment. George favors corporal punishment. George is a traditional teacher.
14. You said you would let us go to recess only if we did all our work, and we did all our work, so now you have to let us go to recess.
15. Teacher: "I can not let you use the phone, because the rule says no one uses the phone during class time."
Student: "Please just for me, I won't tell anyone and I have to make this call before mom leaves for work."
16. All teachers like children. You like children. So you are a teacher.
Mathematical examples for reasoning and proof
Geometric construction as a proof 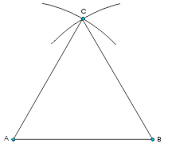
Prove that a construction of a triangle will yield an equilateral triangle. Figure at right shows how a compass can be used to demonstrate how three equal lines can be drawn to create a triangle with all three sides congruent.
An Even number added with another even number it will make an even number.
See three different levels: concrete, semi-concrete, and formal proofs .
Proof of a specific & translate to general
How to argue for an infinite claim.
Learners found the mass of a dry sponge (98 g), then soaked it in water and found its mass (145g). When they were asked to find the mass of the water they wanted to subtract. The teacher asked them to prove it or convince her that it was an accurate solution.
The wet sponge's mass was 145 grams - the dry sponge's mass 98 grams. Students decide to use nice numbers and adjust to subtract. So they subtracted 100g. 145 - 100 = 45. Then they were not sure if they should subtract two more or add two more.
To represent the problem they drew a rectangular shape (sponge) with an enclosed blob to represent the water. They labeled the area outside the blob 98g for sponge and  labeled the blob - water with a question mark. Then they wrote 145g beside the rectangular shape and said that represented the sponge and the water.
labeled the blob - water with a question mark. Then they wrote 145g beside the rectangular shape and said that represented the sponge and the water.
They proceeded to explain that taking 100g away was 2g too much so they would need to add two back.
To get to the generalization the teacher asked this follow up question: Would this always be true for subtraction?
What would the statement be? Or rule?
Like - If you take away smaller you end up bigger so you need to ... Or If you take away bigger you end up smaller so you need to ...
With the hopes to get to the idea of: How to argue for an infinite claim.
Think that problem is too complicated to start?
What if we use the same numbers only change the scenario?
Max has 145 collector cards and gives 98 to Chris. How many collector cards does Max have left?
This can also be solved with subtraction and the numbers are the same as the sponge problem. However, the representation of the problem isn't as complicated because of the type of subtraction problem it is.
Why is there such a difference? The sponge problem is stated as an addition problem with the start and finish numbers know, but not the change. This makes it more complicated than this second which is a start total known and the amount to remove or separate known with the unknown as what is left.
See samples of different addition and subtraction problems
Infinite analogy
The following are examples of specific instances that can use proof by analogy if the analogy is stated as to be infinite.
Prove why you can exchange numbers of equal value with equations of equal value.
- Start with two equal equations 4 + 4 = 2 * 4
- Add 3 to each (4 + 4) + 3 = (2 * 4) + 3
- Will this work for adding any number? If so why?
Prove the validity of this equation:
- 4X + 2Y - 3 = 0?
- Assuming X and Y are integers.
- Not valid, since no matter what value is assigned X and Y they will always (infinity) sum to an even number from which it is impossible to remove an odd integer to obtain 0.
Prove that two unknowns x and y when added together and squared are represented accurately with the following:
- (x + y)2 = (x + y)(x + y) = x2 + xy + yx + y2
- equivalent by analogy (12 * 34) = (10 + 2)(30 + 4) = 10*30 + 10*4 + 2*30 +2*4
- Sample explanation of whole number multiplication and take it to infinity.
Can prove the validity of the distributive property by analogy?
x2 - 1 = (x +1 )(x - 1)
Proof by Exhaustion
Identify all examples and justify their inclusion as well as reasons for the elimination and identification of all possibilities.
Example
What are all of the possible four cube high towers that can be made with red and yellow cubes?
Proof by exhaustion using systematic process of recursion.
Students must take time to build meaning, which must be from concrete experiences. Time to notice patterns between the physical entities and retain these ideas in short term memory long enough to act on them to create relationships and communicate these relationships.
It is the communication element that pushes us to identify the limits, systematically explain all possibilities even if they extend to infinity.
There are several ways to systematically try to insure the discovery of all possibilities of the cube towers. Some examples follow.
First towers can be made to show the number of red and yellow cubes that could be to make a four cube tall tower. Below illustrates that if four cubes are used for each tower it would be possible to build a tower with 4 red, 3 red and 1 yellow, 2 red and 2 yellow, 1 red and 3 yellow or 4 yellow. There is no other combination of reds and yellows for a 4 cube tower.
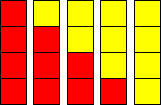 However, that doesn't provide for the different placements of the two colors in different combinations. For example: There is only one way to arrange a tower with all red. Like wise there is only one to arrange a tower with four yellow. However, there are several ways to arrange three red cubes and one yellow cubes. Like wise for two red and two yellow and three yellow and one red.
However, that doesn't provide for the different placements of the two colors in different combinations. For example: There is only one way to arrange a tower with all red. Like wise there is only one to arrange a tower with four yellow. However, there are several ways to arrange three red cubes and one yellow cubes. Like wise for two red and two yellow and three yellow and one red.
These can be found by rearranging the cubes for each of the above combinations of colors and summing the totals 1 + __ + __ + __ + 1 = __ .
Another way is to use a tree. Start with R and Y and put a R Y pair below it and continue till there is a row for each of the four rows in the towers. Then find all the different paths through the maze of connections and label each.
- r, r, r, r

- r, r, r, y
- r, r, y, y
- r, y, r, r
- r, y, y, r
- r, y, y, y
- --------
- y, r, r, r
- y, y, r, r
- y, y, y, r
- y, y, r, y
- y, r, r, y
- y, y, y, y
Another example by exhaustion or discovery is all the examples to find,
How many squares in a 5 X 5 square?
Systematic solution could find the number of 
- 1 X 1 squares
- 2 X 2 squares
- 3 X 3 squares
- 4 X 4 squares
- 5 X 5 squares
Then total the five groups.
See example of card trick explanation using elimination and identification.
Prove the handshake problem
How many handshakes will there be for everyone to shake hands with everyone else in your classroom.
Systematically - if there are five people, the first person shakes hands with the four other people in the classroom. Since the first person has shaken everyones hand, the first person can relax and sit down. The second person has shaken the first person's hand, so the second person begins by shaking the third person's hand. When the second person has shaken everyones hands the person may relax and sit down. The third person now has shaken hands with person one and two, so has to shake the fourth and fifth persons' hands. Then the fourth person only has to shake the fifth person's hand and when it becomes the fifth persons turn, by golly the fifth person has shaken all the hands and is done.
To summarize.
Person five - 4, person four - 3, person three - 2, person four - 1, person five - done - o.
Add them and get: 4 + 3 + 2 + 1 = __ .
Teaching suggestions
Arguments from children's representations (like the 3 + 5 = 5 + 3 ) and from other stories with numbers can be an effective way to move learners toward a proof as a more general idea. The key is for the teacher to facilitate the inclusion of questions such as:
- Will this work for other number?
- Will it work for all numbers?
- If not, then is there a group of numbers for which it will work?
The purpose is to push thinking to generalize an explanation to include all possible examples that are true for all cases, or move to infinity.
Example
A = length * width
Does multiplying length and width determine area for every rectangle and square? Why?
We can use graph paper or tiles to represent a rectangular area. By modeling how every time a row of square tiles is add it is represented by multiplying the number of column by an increased row number of one.
Elementary students will need to act this out multiple times. Talking about how the rows are increasing and the columns are increasing and how that can be represented in the product of the length and width. Then ultimately they should recognize that it doesn't matter what the number of rows or columns are. Therefore, the expression L * W will determine the area. To be able to do so students need to be familiar with all the necessary conditions or characteristics for conservation. Specifically in the case of conservation of area.
Misconceptions and fallacies of inaccurate proofs
- Use of the word proof as a synonym for evidence.
- Think of proof as verification with a single case
- Think solving a problem is the same as a proof
- Can prove by checking single cases
- See this checking of a few cases as the most convincing argument.
- Often don't see the power of generality
- Lack understanding of logic
- Lack problem solving heuristic, strategies, and habits of mind
- Imply a solution is correct if the algorithmic procedure was followed correctly.
- Use authority to justify - My teacher said so. - Lampert (1993) found that students believe: doing mathematics means following the rules of the teacher and knowing mathematics means remembering and applying those rules when the teacher provides a problem and mathematical truth is determined when the answer is judged correct by the teacher.
Ecological fallacy
Ecological fallacy is thinking relationships observed for groups necessarily hold for individuals.
Examples:
- A correlation describes a measured relationship. Correlations of group averages can be much higher than correlations of individual scores. Thinking both are equal is an example of ecological fallacy.
- It is an ecological fallacy when conclusions are made about individuals based only on analyses of group data. Assume you know the average math scores of a specific classroom is the highest in the district. If you meet a student from the class and think she is a math whiz, then that is an ecological fallacy. As her belonging to the class with the highest average score does not mean she has a high-score in math. She could be the lowest math in a class of math geniuses.
- Another ecological correlation fallacy is when people generalize that if something is good for an individual, then it is good for everyone. for example: High scores on tests grant entry to elite universities, therefore high scores must be right for the nation as a whole. Most parents would probably like their children to have high scores. However, looking at our nation as a whole we should come to a different conclusion. In that situation we would want a combination of people that are able to be leaders, followers, heroes, creators, producers, so that the society could function for the benefit of everyone.
Exception fallacy
Exception fallacy is sort of the reverse of the ecological fallacy. It is when a conclusion about a group is made on the basis of a specific case. This fallacious reasoning is often at the core of sexism and racism. The stereotypical response when seeing a woman make a driving error of: "women are bad drivers." Is wrong. Fallacy...
Scoring Guide for proof
Low level
Learners at this level will not provide a logical accurate justification to demonstrate the truth of a proposition or statement.
- They might simply state a proposition is true without any reference to why the proposition is true.
- They might accept a proposition as true, because a teacher, parent, or text says it's true (Harel & Sowder, 1998).
- If they provide a justification, it can be transductive.
- Example.
- The sum of two even numbers is even, because that is just the way it is.
- Yes, the numbers will be equal because they will always be equal.
- They are equal, because we learned it in class.
- They are equal because they are straws.
Learners at this level appear to be aware of the need to provide a logical accurate justification to demonstrate the truth of a proposition or statement. However, their justifications are specific examples from past observations or experiences. Not based on accurate justification that can be generalized to all cases.
- Checks a few cases.
- Systematically checks a few cases (e.g.., even and odd numbers).
- Checks extreme cases or random cases.
- Consider the use of a generic example (proof for a class of objects) (cf. Balacheff, 1987).
Learners at this level are aware of the need for a general argument, and often attempt to produce such arguments themselves; the arguments, however, fall short of being acceptable proofs.
Falling short may happen in one of two ways:
- Express recognition of the need to provide a general argument and attempt to produce such an argument, however, the argument provided is not a viable argument (i.e., the argument is either incorrect or it would not lead to an acceptable proof).
- Express recognition of the need to provide a general argument and attempt to produce such an argument, however, the argument is incomplete (if completed, the argument would be an acceptable proof).
In both situations, the point is that students are attempting to treat the general case. In addition. Level 2 justifications also include responses from those who demonstrate an awareness that examples of a few cases does not suffice as proof. May also express a need to include all cases or express recognition of the limitation of any attempted proof attempted.
Learners at this level appear to be aware of the need for a general argument, and successfully produce acceptable arguments.
- Their arguments demonstrate that a proposition or statement is true in all cases.
- Arguments at this level involve assumptions or givens, a chain of deductions used to build the argument, and finally an explicit concluding statement.
- Arguments may lack a rigor or formality associated with a proof, their arguments, nonetheless, do prove the general case.
Upper level
Adapted from - Middle School Students' Production of Mathematical Justifications. Eric J. Knuth, Jeffrey M. Choppin, and Kristen N. Bieda. In Teaching and Learning Proof Across the Grades. A K-16 Perspective (2009).
Summary
- Research suggests current practice is insufficient and only change can improve people's abilities to reason and use proofs.
- Goswami, and Hatano and Sakakibara (2004, ISBN 0-8058-4945-9.) observed children in natural settings using everyday language while they were attempting to use the language of mathematics while reasoning mathematical. That language was mostly absent of spontaneous analogies. The authors attributed these findings to limitations in a child's mathematical knowledge as well as to the norms and practices in their instructional setting.
- A mathematical community or culture must include many opportunities with experiences that emphasize problem solving, representation, reasoning, and communication, where students make conjectures and develop skill in using these tools of reasoning and proof through systematic representation to justify their ideas.