Multiplication of Fractions with Cuisenaire Rods
Concrete representation for multipliation of fractions
Questioning is the basis of all learning.
Overview
- Introduction
- Becoming Familiar with the Rods
- Representing fractions with Cuisenaire Rods
- Fractional representations
- Introduction to multiplication of fractions
- Overview of the kinds of multiplication of fractions
- Fractional numbers less than one times whole numbers
- Fractional numbers times fractional numbers
- Mixed fraction times mixed
- Summary
Introduction
This page describes multiplication of fractional numbers. It is an update of an article I wrote in 1984 for the Arithmetic Teacher. Understanding Multiplication of Fractions. Robert D. Sweetland, Volume 32: Issue 1.

Becoming Familiar with the Rods
Multiplication is an operation that many learners don't understand it's full significance. When it is combined with fractional values the problem in understanding the operation of multiplication with fractional values takes considerable study with many varied different opportunities. The use of Cuisenaire Rods can be one of these. They can provide concrete proportional representations for number values and operations.
Multiplication with fractional values is explored in this article.

The rods are ten in number and range in length from 1 centimeter to 10 cm.
Each length is identified by a unique color.
White, Red, light Green, Purple, Yellow, Dark green, blacK, browN, bluE, and Orange
The capitalized letters are used to identify the different rods. Notice the pattern uses the initial letter until there are three "B's" so the ending letters are used and then back to the initial for Orange.
If, then activities to become familiar with the use of Cuisenaire rods for whole, decimal, and fractional numbers
Representing fractions with Cuisenaire Rods
To represent fractions, or operations with fractions, with Cuisenaire rods, a rod, or combination of rods, needs to be selected for one whole or a unit value.
Below are a few of the infinite possibilities that can be used as a whole or a value of one.
Tasks that use concrete models provide opportunities for students to learn how to create mental representations from the visual aspects of the concrete models. These mental representations are necessary for understanding fractions and their operations.
Fractional representations
Example with a shorter notation.
How would you complete these five?
Answers:
- W = 1/2
- G = 1/3
- R = 2
- R = 2/3 and D = 2
Fractional representations greater than one
 As learners become good with fractions, less than one, then they should be given problems with whole numbers and fractions greater than one, mixed numbers.
As learners become good with fractions, less than one, then they should be given problems with whole numbers and fractions greater than one, mixed numbers.
How would you complete these?
Answers:
- 2
- 3
- 4 1/2
Introduction to Multiplication of Fractions
Multiplication of fractions can be classified into four groups. Let's briefly look at each type to see the relationships between the factors and the products.
Later, we will look at each type in more detail and some instructional aspects.
First: multiplication of a fraction and a fraction.
When a fraction less than one is multiplied by another fraction less than one, the results is a product less than either factor.
For example, imagine this problem:
A person has half a candy bar and shares it with a friend. How much does each person get?
1/2 of a 1/2 a candy bar = 1/4 candy bar.
Set up three ways with Cuisenaire rods:

In multiplication of whole numbers, the product is always greater then either of the factors.
Here the product is less than either factor. This can be a problem for students that believe multiplication always results in products greater than the factors.
Second: multiplication of a whole number and a fraction
The second type is a whole number multiplied by a fraction.
For example, after the kids were done eating pizza there were only three boxes with any pizza left and each had about 1/4 of a pizza in it. How much pizza was left?
3 boxes × 1/4 pizza = 3/4 pizza
Set up with Cuisenaire rods:
Third: multiplication of a mixed number and a fraction
The third type is factors of a mixed number and a fraction. The value of this product is between the two factors, unless one of the factors is equal to one; then it equals the other factor. Problems of this type still don’t fit the false assumption that multiplication produces products greater than the factors.
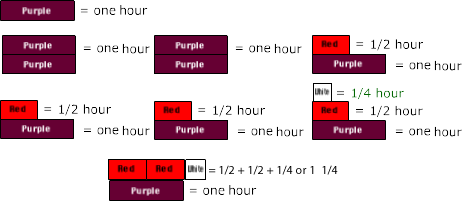
Mom says that I can watch half the movie, then do chores, and when the chores are done, I can watch the rest. The movie is two and one-half hours long. When do I have to do chores if I start to watch the movie now?
1/2 of 2 1/2 hours = 1 1/4 hour
Fourth: multiplication of a mixed number and a mixed number
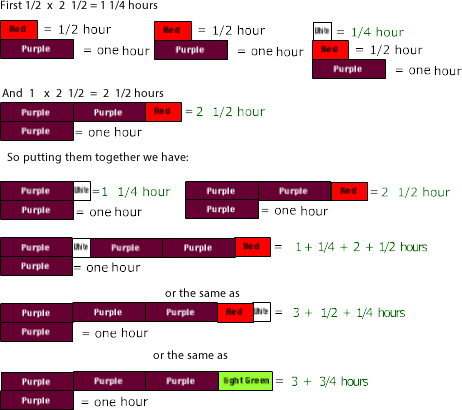
The fourth type is both factors are mixed numbers and the product is larger than either factor. For example,
Juan rents two movies each two and one-half hours long. He has watched one and one-half before he leaves to go to practice. How many hours of movies has he completed (watched)?
1 1/2 of 2 1/2 =
Overview of the four kinds of multiplication of fractions
The four comparisons explored above:
- Fraction multiplied by a fraction: 1/2 * 1/2,
- Whole number multiplied by a fraction: 2 * 1/2 or fraction multiplied by a whole number 1/2 * 2,
- Fraction multiplied by a fraction: 1/2 * 1 1/2 or mixed number multiplied by a fraction: 1 1/2 * 1/2, and
- Mixed number multiplied by a mixed number 1 1/2 * 1 1/2.
These are derived partly by the physical appearance of the numerals for each factor.
However, there is also a relationship between the values of the product and factors. The products are not only smallest when the factors are smallest, but the magnitudes of those products are less than the factors themselves. This is interesting and helpful to know.
For example:
Factors less than one:
- 1/2 of 1/2 = 1/4
- 1/2 * 2/3 = 1/3
- 1/2 x 1/5 = 1/10
- 1/2 * 1/4 = 1/8
One factor less than one and the other greater than one:
- 1/2 of 2 = 1
- 1 /2 x 3 = 1 1/2
- 1/2 * 1 1/2 = 3/4
Both factors are greater than one:
- 1 1/2 * 1 1/2 = 2 1/4
- 1 1/2 x 2 1/2 = 3 3/4
- 1 1/2 of 2 = 3
One factor is one:
- 1/2 of 1 = 1/2
- 1 * 2 1/2 = 2 1/2
- 2 1/4 x 1 = 2 1/4
Instructional suggestions
When teaching multiplication of fractions most educators begin with multiplication of fractions less than one and whole numbers. Usually finding fractional parts of whole numbers that will result with nice products (1/2 x 4 = 2, is nice, 1/2 of 5 not so nice).
Then progress to whole numbers multiplied by fractions: 4 * 1/2 = 2.
Followed with both fractions being less than one 1/2 of 1/2 = 1/4. Once students learn how to solve these types of problems, too many teachers believe students can generalize a procedure that works for multiplying fractions of all types. This practice, lack of understanding of multiplication of fractions leaves most people unaware of understanding multiplication of fractional numbers and the different relationships of the factors and products.
Cuisenaire rods help students create and generalize mental representations to extend their understanding of fractions to the operation of multiplication with fractions, and the relationships that are created.
Setting up and solving problems for fractional numbers less than one times whole numbers
Let's start with 1/3 of 3.
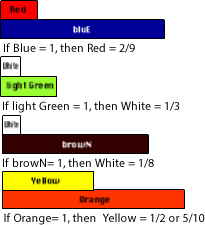
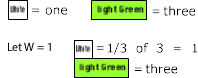 The first thing to do is decide what to use to represent one. If White is selected as one, then light Green will have a value of three, because three Whites make a light Green, therefore, one-third of a light Green rod can be represented by a White and we already know White is one so 1/3 of 3 = 1.
The first thing to do is decide what to use to represent one. If White is selected as one, then light Green will have a value of three, because three Whites make a light Green, therefore, one-third of a light Green rod can be represented by a White and we already know White is one so 1/3 of 3 = 1.
Let’s look at another with a product that is larger than one, 1/3 of 6 = 2.
 Again the first thing to do is decide what to use to represent one. If we select White as one, then light Green has a value of six. Three Reds make a Green, therefore one-third of light Green is a Red, because White is one, then Red would be two.
Again the first thing to do is decide what to use to represent one. If we select White as one, then light Green has a value of six. Three Reds make a Green, therefore one-third of light Green is a Red, because White is one, then Red would be two.
Let's try a problem with a product less than one, 1/3 of 1.
Chi has a one pound package of ground meat and wants to make three hamburgers.
To let White represent one would mean that we wouldn't have any rods smaller than white to use to represent the three hamburgers. To solve this problem select a rod, larger than one, to use for the one pound package of meat so there are smaller rods to use to represent the hamburgers.
![]() Students who have used the rods before will recognize that if they let light Green = 1, then White can be used to represent the hamburgers, because 3White rods = 1Green rod. Therefore, light Green is one in this representation and White is less than one, or 1/3.
Students who have used the rods before will recognize that if they let light Green = 1, then White can be used to represent the hamburgers, because 3White rods = 1Green rod. Therefore, light Green is one in this representation and White is less than one, or 1/3.
Students need several experiences with problems that multiple fractional values less than one and whole numbers with rods as well as with other manipulatives and representations.
The biggest difficulty for students is being able to relate fractional values and whole values to the same rod and fluently switching from problem to problem. This is a developmental milestone that students struggle to acquire for understanding fractions, place value, multiples, and other mathematical ideas.
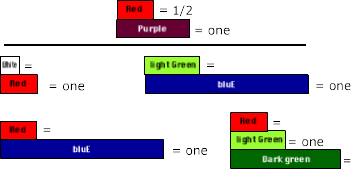
Setting up and solving problems for whole numbers times fractional numbers less than one
Previous examples included a fractional part less than one times a whole number with the value of one and larger: 1/3 × 3 = 1, 1/3 × 6 = 2, and 1/3 × 1 = 1/3
However, examples for whole numbers times fractional numbers less than one: 3 × 1/3 = 1, 6 × 1/3 = 2, and 1 × 1/3 = 1/3 were not included.
While students who understand the properties of multiplication can use the commutative property and rationalize three times one-third is equal to one-third of three (3 * 1/3 = 1/3 * 3) and similarly for others. There is a difference in the way these problems arise in the world and are represented.
Being able to understand, represent, and solve problems with fractional values and the operation of multiplication requires more than knowing 3 * 1/3 = 1/3 * 3 by the commutative property.
So let's look at an example with a whole number and fraction with a value less than one.
Kate has three videos. Each is one-third of an hour long (20 minutes). If she watches them all back to back, how much time will it take?
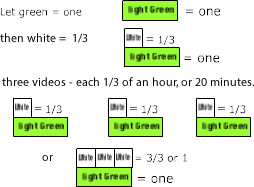 For this problem one-third of an hour needs to be represented three times. If light Green represents one hour, then White can represent one-third of an hour.
For this problem one-third of an hour needs to be represented three times. If light Green represents one hour, then White can represent one-third of an hour.
The problem requires three Whites, one for each of the one-third hour videos. Three-thirds of an hour or 1hour.
More fractional numbers less than one times whole numbers
You might be thinking the examples have been fitting with the sizes of the rods and wondering what happens when the fit isn't so good.
Let's see how to set up such a problem as one-third of five.
- What is one-third of five fingers? (gross?)
- If I have five bags of potting soil and want to put one-third into each of three pots how many bags go into each?
 Since light Green is the first rod that we know that can be matched with three other rods (three White) we can use it for one. If light Green is thought of as one, then five light Green rods represent five. Five light Green rods or a combination of Orange and Yellow also represents five light Green. Either way a Yellow rod will be 1/3 of five light green or an Orange and Yellow combination.
Since light Green is the first rod that we know that can be matched with three other rods (three White) we can use it for one. If light Green is thought of as one, then five light Green rods represent five. Five light Green rods or a combination of Orange and Yellow also represents five light Green. Either way a Yellow rod will be 1/3 of five light green or an Orange and Yellow combination.
Another...
You have probably noticed all the examples have only one fractional part or the numerator is one. It is also possible to represent fractional numbers less than one, with multiple fractional parts (numerator greater than one), multiplied by a whole number.
Example 1
Mike had ten dimes and gave three-fifths to Josa. How many did Josa get?
 Three-fifths of ten. Need to represent a group of ten dimes. If White represents one dimes, then Orange represents ten. One fifth is Red so three-fifths is three Red with one Red equal to two dimes and three would make six dimes.
Three-fifths of ten. Need to represent a group of ten dimes. If White represents one dimes, then Orange represents ten. One fifth is Red so three-fifths is three Red with one Red equal to two dimes and three would make six dimes.
Example 2
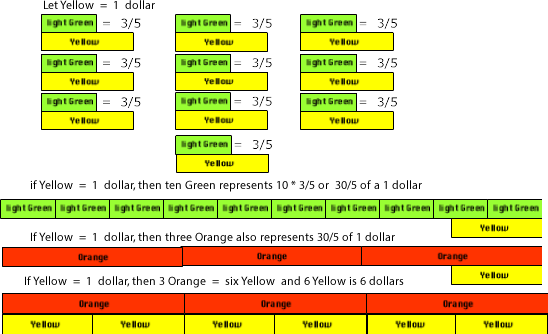
There was a group of eleven children going to a movie, when one of them noticed they had lost the money to get into the show. The other ten decided that if each gave three-fifths of a dollar to that eleventh person, it would be enough for them to buy a movie ticket. How much was that person given? (10 × 3/5).
Let’s try two ways: 3/5 × 10 and 10 × 3/5:
 If we let White represent one dollar, then Orange would be ten dollars. One-fifth of Orange is Red so three-fifths is three Reds. The dollar value was set as White equals one dollar. Therefore, Orange equals ten dollars, Red equals two dollars, and three Reds equal six dollars.
If we let White represent one dollar, then Orange would be ten dollars. One-fifth of Orange is Red so three-fifths is three Reds. The dollar value was set as White equals one dollar. Therefore, Orange equals ten dollars, Red equals two dollars, and three Reds equal six dollars.
A second way to represent it would be to represent three fifths of a dollar with a light Green, take ten of them, and find the value for all ten.
Example 3
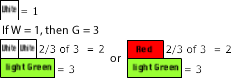
Dad is always trying to make people think so he says things like there are three packages on the table you need to take two-thirds of them (2/3 × 3). How many did I need to take?
Let’s try this the same two ways: 2/3 × 3 and 3 × 2/3:
First two-thirds of three:
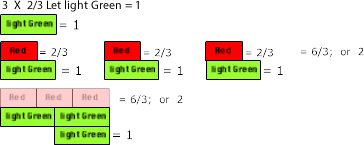
Second three times two-thirds or three groups of two thirds:
For 3 x 2/3.
Green was selected to represent one.
If Green = 1, then Red = 2/3
Therefore, three red rods represents three groups of two-thirds.
Summary
Students find it more difficult to work with fractional parts greater than one/part (1/2, 1/3, 1/4, 1/5 ...). It takes time for them to generalize their understanding of one-third to two-thirds and other multiple fractional parts for other fractions.
Students need to be given time to connect their previous understanding of addition and multiplication of whole and fractional numbers. When they are they will realize that two-thirds can be thought of as two times one-third or one-third added twice.
To acquire understanding of fractional values, with a factor that has a numerator greater than one, we must know it is a multiple of the unit of the fractional part. For example three-fifths is a multiple of one-fifth. Therefore, three-fifths has factors of 3 and 1/5.
Previous experiences with multiples, skip counting, multiplication as row and columns, area, rectangles, squares, and repeated addition are essential to understanding fractions and multiplication.
Fractional numbers less than one multiplied by a fractional number less than one
Proper fraction times a proper fraction, but I don't like to call fractions proper and improper. They are fractions and sometimes one is more useful than another, but that usefulness can only be determined by the use and not the form in which the number is in.
You surely have realized that knowing what to represent as one is key to arriving at an accurate solution. Any real life or world problem requires a unit value to be selected for each problem to represent the value of one. It really helps to note this as part of the representation so everyone knows the values that have been assigned.
Let’s see some examples of how fractional numbers less than one are multiplied by a fractional number less than one.
Example 1:
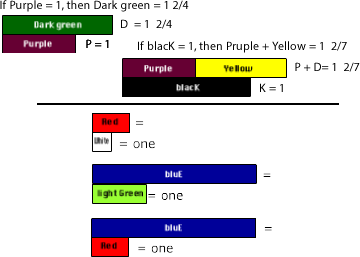
My dad, brother, and I mowed the neighbors yard. My brother and I each mowed one-half of the front yard, which dad said was two-fifths of the whole yard. How much of the whole yard did I mow? 1/2 of the front which is 2/5 of the whole yard.
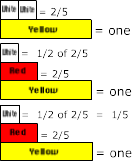 First, decide what to use as one so that two-fifths can be represented.
First, decide what to use as one so that two-fifths can be represented.
Next, ask what one-half of the two-fifths is and represent it.
Then, determine the value of White if Yellow is one. Students may need to be reminded to ask what part of the whole (ones rod or unit) does the top rod represent. In this case white is both 1/2 of 2/5ths and 1/5 of Yellow or one. This is a problem for many young children. Objects that have equal simultaneous values.
You may be wondering how students are to select a rod for the unit (one). For the problem we just did we knew we want to make two-fifths so it makes sense to select a rod that can be used to represent fifths. There are only two rods from which to select: Yellow and Orange. If you haven’t used the Cuisenaire rods before, knowing this will take some thinking. Those who have experienced them for a few hours thinking about what rods can be used to make trains to match other rods, will know what colored rods can used to evenly match others. It may even be helpful to challenge students to make a list or table of these relationships.
So for this problem we used Yellow, but let’s see how it would have been represented if it had been Orange.
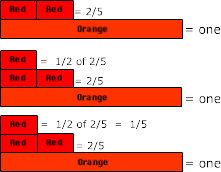 First, we decide to use Orange as one so two-fifths is represented with Red.
First, we decide to use Orange as one so two-fifths is represented with Red.
Next, ask what one-half of the two-fifths is and represent it with Red.
Then, determine the value of 1/2 of 2/5. Since Orange is one, then Red is 1/5 of it. Again many students will need to be reminded to ask what part
of the whole (ones rod or unit) does the top rod represent.
When selecting something to represent one, or the unit, by thinking about what rods match other rods isn’t working, then this simple rule will always work:
First try using the denominator of the second factor. If that doesn’t work, multiply the denominators and determine what rod or combination of rods would be needed to equal the length (cm) of that many Whites.
For example if the problem was 2/3 × 4/5. Yellow would be the first choice, but 2/3 of yellow can’t be represented with whole rods. So 3*5 =15, and three Yellows or an Orange and a Yellow can be used for one. Two-thirds can be represented with two Yellows).
Don’t tell this to students. Tell them to think about the size of pieces they want to use. If that doesn’t help, then suggest what will. Finding the unit rod can be fun and challenging, but if students are told to multiply denominators, some will continue to do this even when it isn’t desirable. For example, 1/5 x 5/9. If the denominators are multiplied (45), then four Orange rods and one Yellow rod would represent one. This combination will work, but using bluE makes a better representation to facilitate conceptual understanding which will facilitate students’ problem solving and mathematical fluency. Learning rules, without conceptualization, is procedural knowledge without knowing when or how to use it.
Another example
This example is the most complicated type of problem of proper fraction multiplied by another proper fraction. These should be avoided until students have mastered the others.
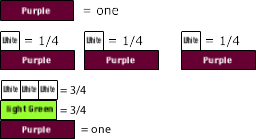
Mary was given a bag of candy by her mother and told to share it with her brother and sister. When her brother saw her with the candy he asked if he could have some. Mary told him he could, but she was to share it between the three of them. So she and her brother divided it into three equal groups, Her brother took his share and left Mary with two-thirds left in the bag. When her sister found there was candy she went to Mary and asked for her share. Mary again said she was told to divide it into threes and share it. So they divided it into three equal groups, her sister left with hers and Mary put two-thirds in the bag. How much of the original bag of candy did Mary end up getting?
The problem :
The candy left after her brother and sister were given a share is 2/3 of the candy left after giving her brother a share and leaving Mary with 2/3 of the original bag.
First think that you want to fine two thirds of a bag that has two thirds of what was in the original bag (2/3 bag of 2/3 bag). 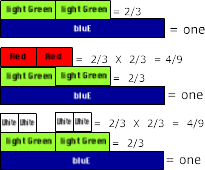
Then decide to Let bluE = one and find two-thirds of blue. Two light Green.
Then find two-thirds of the light Green (2/3 of 2/3).
This can be thought of two ways.
- light Green represents 2/3 of bluE and Red represents 2/3 of the two light Greens that are being thought of as one Dark green
- light Green represents 2/3 of bluE and White represents 2/3 of light Green
The complexity of understanding multiplication of fractions is related to recognizing the pieces and the wholes, and how they relate and change depending on their values and the operation of multiplication.
An example of this duplicity of values is when the two light green rods are used as two pieces (2/3) and also used together as a unit (2/3) to determine what two-thirds of it is.
To understand these relationships takes considerable time for students to experience, interpret, construct understanding, and connect those understandings. One way to provide time for sufficient experiences is to either delay teaching multiplication of fractions procedurally or to stop teaching it procedurally completely and let student invent their own algorithmic procedures.
To understand why the products of fractions are so varied. The use of concrete representations help students understand why and begins to provide a variety of approaches for thinking about problems.
Mixed fraction multiplied by mixed fractions
Problems with mixed fractions multiplied by a mixed fraction can be solved by multiplying the four factors and adding the products. While this idea is essential to the understanding of multiplication it isn’t as evident when a standard algorithm is used to solve these kinds of problems.
Let's see how the previous ideas can be combined to multiply mixed fractions:
Example 1 1/2 × 2 1/2:
First, identify the factors that need to be multiplied.
Then decide how to represent one.
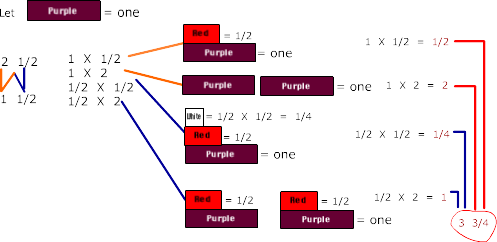
Once it is decided how one will be represented, the problem can be set up by multiplying the four pairs of numbers: 1 x 2, 1 x 1/2, 1/2 x 2 and 1/2 x 1/2. As illustrated above.
However, when a person understands how multiplication of fractions works, they will be able to find all kinds of short cuts. For example: in the problem 1 1/2 times 2 1/2 it can be solve mentally by thinking:
1 × 2 1/2 = 2 1/2 and 1/2 × 2 1/2 = 1 1/4.
Then combining 2 1/2 + 1 1/4 to get 3 3/4
Another example: 12 1/4 × 12 1/4
12 × 12 = 144
12 × 1/4 = 3
1/4 × 12 = 3
1/4 × 1/4 = 1/16
144 + 3 + 3 + 1/16 = 150 1/16
I believe this is easier than using the traditional algorithm and having to multiple 49 x 49 and divide that product, 1401, by 16 and more importantly it comes with understanding.
Students who have sufficient concrete experiences will understand all methods, and have the confidence and ability to select a strategy based on accurate mental images. The algorithm doesn't help students understand multiplication of fractions conceptually. So while it may be quicker, one needs to understand why the pairs of numbers must be multiplied, and what it means for each type.
Summary
Some students are always wanting a rule to memorize, because they have given up on the idea that they can understand mathematics, or they can’t see any advantage to solving problems other than with rules. They find all they usually have to do is take the rule and use it when they are presented with problems already set up on work sheets, but life doesn't present problems in this manner.
By presenting problems in real situations and challenging students to understand their world most students will invest time and work to learn how to use math to understand and explain the world.
Presenting challenging problems and enough carefully chosen problems, such as:
2/3 × 4/4
Students who use the rule end up with more work, whereas those who take time to study the problem think
4/4 = 1
And leap to the answer.
Other problems like the following:
1/2 × 22/36
1/3 × 9 3/8
2/3 × 27
9 1/3 × 9 1/3
Encourage students to understand the multiplication of fractions.
The use of the rods is but a beginning.