Division of Fractions sample problems
See also Concepts
Problem

Solution A
Symbolic representation
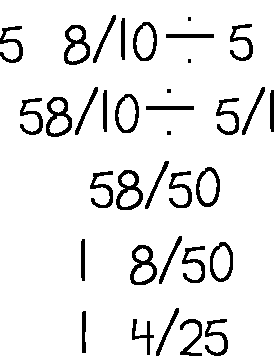
This person wrote the eight-tenths as a fraction, used a fractional division algorithm and reduced the fractional answer to the least terms. Accurately found a solution, but couldn't draw a representation. Used symbolic reprentation.
Solution B
Reduced fractional part and found five equal parts of 5 4/5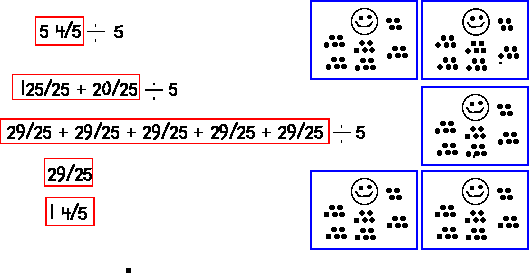
This person thought of eight-tenths as a fraction, reduced it, found a common multiple for 4 and 5, changed both fractions to twenty-fifths, realized that would make five groups of 29/25, took one group, reduced it to simplest terms, and drew pictures to show each person would get 29 pieces with each piece being 1/25.
Solution C
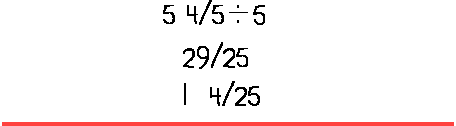
This person took eight-tenths as a fraction, reduced it to 4/5, changed 5 4/5 to an improper fraction 29/5, multiplied by the recipricol of 5, and reduced 29/25 to least terms.
Solution D

This person wrote five and eight tenths as a decimal and divided with a decimal division algorithm, wrote as a fraction, and reduced to lowest terms.
Solution E

This person wrote five and eight tenths as a mixed fraction, changed to improper fraction of tenths, changed to a decimal number, divided using a decimal division algorithm.
Solution F
| Each person gets | Total for all five | Counting back from $5.80 |
|---|---|---|
| $1.00 | $1.00 * 5 = $5.00 | $5.80 - $5.00 = $ .80 |
| $ .10 | $ .10 * 5 = $ .50 | .80 - .50 = .30 |
| $ .0 | $ .05 * 5 = $ .25 | .30 - .25 = .05 |
| $ .01 | $ .01 * 5 = $ .05 | .05 - .05 = 0 |
| Total $1.16 | Total $5.80 | 0 |
This person wrote five and eight tenths as a decimal number, changed it to $5.80, divided the money by thinking of the largest bill or coin that could be given to five people, wrote that amount, subtracted the total for five people from the starting amount, and continued until all the money was used. Then added the amounts given to one person.
Semi-concrete representation.
Solution G

This person thought of five and eight tenths as a decimal, drew a representation for five and eight tenths to include a representation of five and 80 hundredths (green represents crossed out pieces).
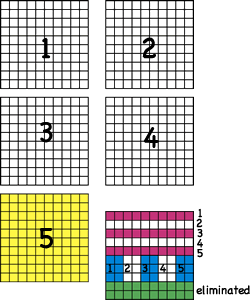
Next this person divided the remaining area into five equal areas. The biggest area included the five big squares (one is yellow), one of five long narrow rectangles (purple stripes), and one of five shorter wider rectangles (blue stripes).
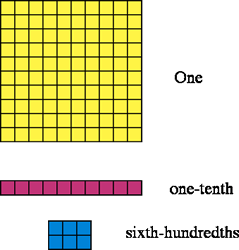
Concret representation.
Each gets 1.16 meters of paper or 1 meter and 16 centimeters.
Solution H
Thought of five and eight-tenths as 5.8, ignored the decimal and thought of multiples of five
| 5 * 10 = 50 |
| 5 *11 = 55 |
| 5 * 12 = 60 |
With this information a student could proced in three ways:
1. Thought 58 is 55 + 3, Therefore a fifth of 55 is 11 and a fifth of 3 is 3/5. Since 3/5 is 6/10, together they are 11 and 6/10 or 11.6. But since we ignored the decimal the answer is ten times what it should be so the answer needs to be divided by ten and you get 1.16
2. The same can be done if you work backwards from 12 and 60. A fifth of 60 is 12 and a fifth of 2 is 2/5 or 4/10. Together it would be 12 - .4 = 11.6. But since we ignored the decimal the answer is ten times what it should be so the answer needs to be divided by ten and you get 1.16
3. Make the same chart and add places for numbers between 55 and 60. The values between 11 and 12 increase incrementally and the only value that could work would be .2 (11.0, 11.2, 11.4, 11.6, 11.8, 12.0). So the value with 58 would be 11.6. However, that value needs to be divided by one tenth as we ingnored the decimal.
| 5 * 10.0 = 50 |
| 5 * 11.0 = 55 |
| 5 * 11.? = 56 |
| 5 * 11.? = 57 |
| 5 * 11.? = 58 |
| 5 * 11.? = 59 |
| 5 * 12.0 = 60 |
Discussion: ...
Mind boggler:
- How many dimes in $2.00?
- 2 ÷ 1/10 = 20 Draw a representation.
Enjoy!