Area model for multiplication & to develop a traditional multiplication algorithms and its connection to algebra
Connecting multiplication in arithmetic to algebra with area patterns
We don't need no more rappers don't need no more basketball players, no more football players. We need more thinkers. We need more scientists. We need more managers. We need more mathematicians. We need more teachers. WE NEED MORE PEOPLE WHO CARE. Tupac Shakur
Overview
Overview
Area or grid, array or matrix models can be used to represent two digit multiplication in arithmetic, multiplication of binomials, represent polynomials, and area models for squares.
Background
Development of multiplication with grids, arrays, and matrices
Area model for multidigit multiplication
Let's walk through an area model to represent the multiplication problem:
23 * 18.
Start with a real life problem
I went to the bakery to get some cookies and found a shelf with discounted bakery items.
On the shelf were eighteen containers of cookies with twenty-three cookies in each. Each was labeled two dozen cookies with a big X over the two dozen and 23 written above it.
I guess they didn't want to sell them and take a chance of disappointing a customer.
I bought all 18 containers so how many cookies did I buy?
Setting up a representation
Draw a visual to represent the problem.
An area array that represents containers and cookies.

Or a person could simplify it without the cookies and outline 18 columns for containers with 23 rows for cookies.
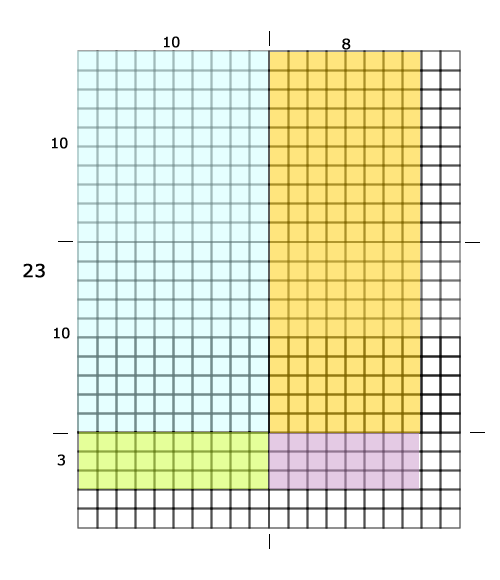
- The 18 columns represent the containers.
- The 23 rows represent the 23 cookies in each container.
Solving the problem
We could count all the cookies in the drawing (chart, graph, matrix).
Or ...
We could use a nice number strategy:
And change the problem from 18 containers of 23 cookies.
To 20 containers of 23 cookies.
This would make it easy to double 23 to 46 and multiply by ten to get 460 cookies.
Then adjust it back to the original problem by subtracting two groups of 23 cookies that aren't needed, as there are only 18 containers.
Or ...
460 cookies - 46 cookies = 414 cookies.
Okay.
Now we know the answer.
How can an algorithm be invented?
Solving the problem (2 digit) with an algorithm (traditional)
We can use the area model to explore and show that all the digits of each factor in a multiplication problem are multiplied with each other.
In other words if we have a two digit factors like above, we will have four multiplications.
Therefore, when we multiple two - two digit numbers, we must know, or discover, all four digits need to be involved.
This is very different from addition and subtraction algorithms.
This idea is illustrated in a simpler problem such as 12 * 3:
Where the three is multiplied by both 10 and 2.
(10 * 3 + 2 * 3)
Unlike addition where the three is only added with the two: 12 + 3; 15.
When we continue this logic for our problem (23 * 18) we need to ...
Decompose both numbers into: 20 + 3 and 10 + 8 and multiply all four numbers.
For example:
| Two tens (20) & three ones | 2 | 3 |
| One ten (10) & eight ones | 1 | 8 |
Multiplied we get:
| Eight times three | 8 | * | 3 | = | 2 | 4 | |||
| Eight times twenty | 8 | * | 2 | 0 | = | 1 | 6 | 0 | |
| Tens time three | 1 | 0 | * | 3 | = | 3 | 0 | ||
| Ten times twenty | 1 | 0 | * | 2 | 0 | = | 2 | 0 | 0 |
4 |
1 |
4 |
Why?
What does all this mean?
Let's explore what was multiplied and how each is represented in the rows and columns with the area model.
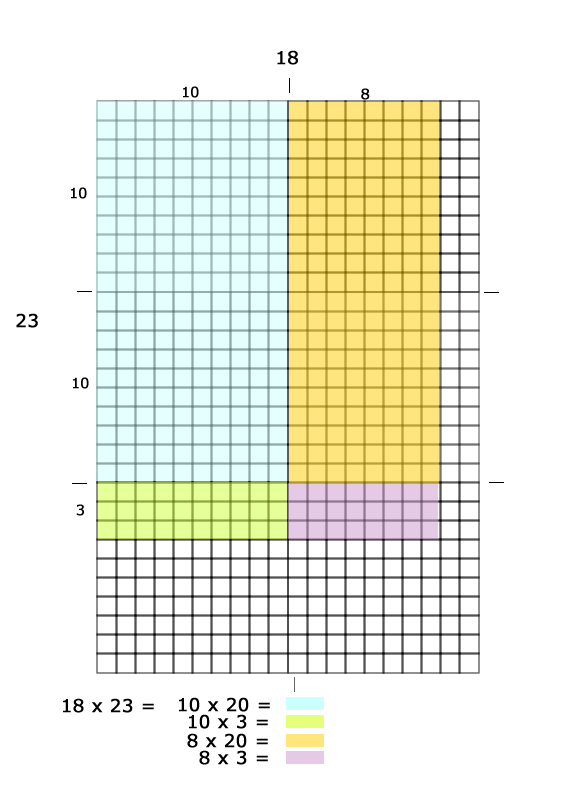
- Ten times twenty is represented by blue.
- Eight times twenty is represented yellow.
- Ten times three is represented green.
- Eight times three is represented purple.
OKAY ...
Let's review what was multiplied:
23 * 18 =
(20 + 3) * (10 + 8)
| First factor | 20 | + | 3 |
| Second factor | 10 | + | 8 |
Multiply all values for all places:
| First digit from the first factor (3) times the first digit of the second factor (8) | 8 | * | 3 | = | 24 |
| First digit from the first factor (8) times the second digit of the second factor (2 with a value of 20) |
8 | * | 20 | = | 160 |
| Second digit from the first factor times (1 with a value of 10) the first digit of the second factor (3) | 10 | * | 3 | = | 30 |
| Second digit from the first factor (1 with a value of 10) times the second digit of the second factor (2 with a value of 20) | 10 | * | 20 | = | 200 |
| 184 | + | 230 | + | 414 |
Sweet!
Grab some graph paper and set up some of your own:
Maybe:
You are going to have tournament. You are planning for 24 teams with each team entering 12 players. You want to know how many total players that will be.
If you give a ribbon to each player on a team that costs $0.89 how much would that cost?
Brain buster!
Use the concepts of place value and a modified area model to explain how David solved the following problem.
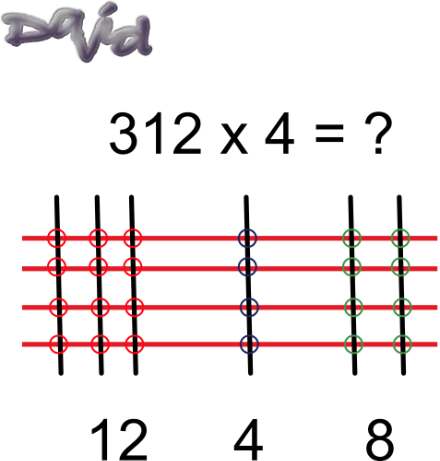
Hint:
Put the following two ideas together.
- Think of the groupings as place value.
- Think of the intersections with the circles in comparison to the squares in an area model.
Two digit multiplication's relationship to binomials
Okay. so why is this important to know and understand to understand algebra?
Well ...
To understand multiplication of binomials ...
Here we go !
Rule for multiplication of binomials
(X + Y) * (X + Y)
- First digit from the first factor times
the first digit of the second factor
(First - F) - First digit from the first factor times the second digit of the second factor
(Outside - O) - Second digit from the first factor times the first digit of the second factor
- (Inside - I)
- Second digit from the first factor times the second digit of the second factor
(Last - L)
Let's see it step by step!
| First factor | x | + | y | |||
| Second factor | x | + | y |
| First digit from the first factor times the first digit of the second factor (F) |
x | * | x | = | x2 | |
| First digit from the first factor times the second digit of the second factor (O) |
x | * | y | = | xy | |
| Second digit from the first factor times the first digit of the second factor (I) |
x | * | y | = | xy | |
| Second digit from the first factor times the second digit of the second factor (L) |
y | * | y | = | y2 | |
| -- | - | --- | - | -- | ||
| x2 | + | 2xy | + | y2 |
Let's see it in an area model ...
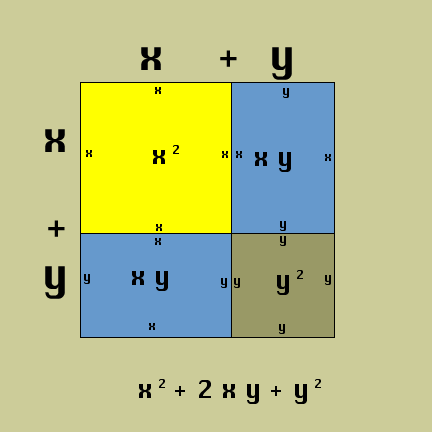
Sweet!
Now I see why elementary and middle level teachers, who teach beyond algorithmic use, are important for the successful development of their mathematical learners?
Brain buster: Try 122
- 122
- (10 + 2)2
- (10 + 2)(10 + 2)
- 102 + 2*2*10 + 22
- 100 + 40 + 4
- 144
Sweet!
Make some of your own or try some examples below.
Enjoy!



- Graph paper
- 2 cm with a 9 x 11 grid.