Sixteen Colored Squares in an Eight by Eight square problem
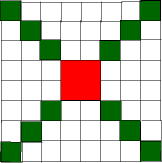
How many different patterns can be made by moving the squares in a way that there is always one square in each corner and two squares in every row and column?
Some grids to diagram the 36 inside squares




Hint: Guess and check. Find a pattern. Solve similar and simpler problem.
Discussion:
Start with a larger image.
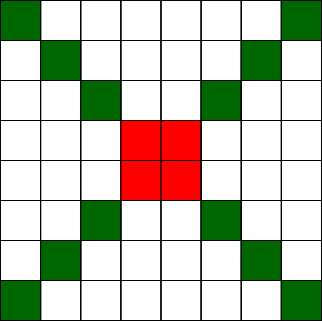
If the squares in the corners can't be moved, then the six by six square is the only area where squares can be manipulated.
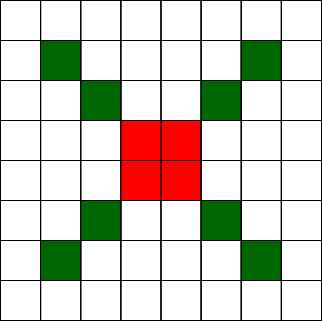
 Within that area squares can be organized in three ways:
Within that area squares can be organized in three ways:
- 1 x 1 Square with an area of 1 square unit, represented as green
- 1 x 2 Square with an area of 2 square units, represented as blue
- 2 x 2 Square with an area of 4 square units, represented as red
There can't be a 3 x 3 square area colored as that would put more than two squares in a row or column.
Could solve by finding all ways to arrange squares so there are two in each row and two in each column.
Then might be able to check or solve by finding the number of ways to arrange squares so there are two in each column and row for smaller squares>
1 x 1, 2 x 2, 3 x 3, 4 x 4, 5 x 5, 6 x 6, 7 x 7 , and 8 x 8.
Possible?
- 1 x 1 not possible, because there wouldn't be 2 squares in a row and column
- 2 x 2, there is one way to have 2 squares in both columns and rows, the red square.
- 3 x 3 square is not possible. No matter how the squares are moved there is no position that a sixth square can be colored that puts two squares in each row and column without having three squares in a row or column.
- 4 x 4 See below
- 5 x 5 not possible
- 6 x 6 See below
- 7 x 7 not possible
- 8 x 8 This problem limits the placement to the corner squares. Therefore, pattern doesn't apply.
4 x 4 square ... or sixteen square ...
Start with the largest pattern:
Two red:
4 + 4 Two ways


One red and two blue:
4 + 2 + 2 Four ways
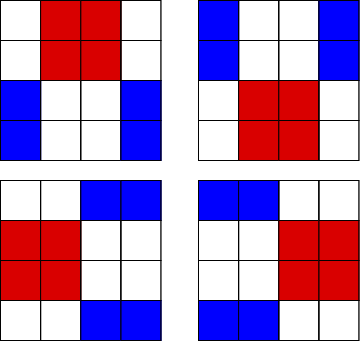
One red, one blue, and two green:
4 + 2 + 1 + 1 Zero ways
One red and four green:
4 + 1 + 1 + 1 + 1 One way

Four blue:
2 + 2 + 2 + 2 Five ways


Three blue and two green:
2 + 2 + 2 + 1 + 1 Twenty Ways

Two blue and four green:
2 + 2 + 1 + 1 + 1 + 1 Fourteen Ways

One blue and six green:
2 + 1 + 1 + 1 + 1 + 1 + 1 ... 4 ways

Eight Green:
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 Two ways

Total 52
Did I miss any?

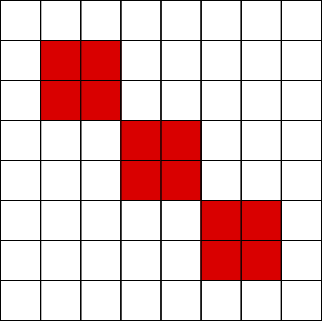
6 x 6 square
4 + 4 + 4 Two ways

4 + 4 Two ways


4 + 2 + 2 Four ways
...
90 ways?
Mind boggler:
Enjoy!