Even, odd, and super even patterns exploration and investigation activities
Page Overview:
- Overview
- Concepts & outcomes
- Math & science content concepts & outcomes
- Problem solving & inquiry concepts & outcomes
- Pedagogical ideas
- Activities
- Groups of pairs - even, odd, multiple of three
- Groups of squares - even & odd groups of squares
- Odd & Even Beads - groups of beads
- V patterns - odd patterns
- Even & odd numbers
- Super even numbers
- Expansion ideas
Overview
Even and odd patterns are recognized by very young learners. They are interesting and used by children when they are playing. Usually when they pair objects evenly or have a left over. Additionally, when lining blocks or objects in lines and find they can be represented and counted by skip counting: 2, 4, 6, … Numbers in this sequence are super even.
This page includes information to plan and use activities for odd, even, and super even patterns and numbers. It includes concepts in mathematics for: patterns, algebra, representation, diagrams, geometry, problem solving, reasoning, visual representation,
Pattern is a repeated design, sequence, structure, change of properties, shape, position, or changing of quantity.
Concepts and outcomes
Mathematical
Concepts
- Patterns can be represented with words, pictures, symbols, numbers, tables, diagrams, charts, graphs, equations, formulas, models, simulations, animations, videos
- Different ways to communicate and represent patterns have different advantages.
- Even is a number which can be divided by two evenly.
- Odd is a number which has one left over when divided by two.
- Pairs are groups of two.
- Arrangements and symmetry of patterns can be used to identify even and odd groups.
- Even patterns can be described as pairs.
- Even and odd par
- Formula is an equation that states a rule about a pattern.
- Sequence is an order in which numbers or things follow each other.n
- Super even numbers are numbers when repeatedly divided by two will result in a quotient of one.
Mathematical concepts, misconception, and outcome knowledge base
Outcomes
- Identify a pattern and group as even or odd.
- Extend patterns.
- Reason and explain patterns as odd or even using pairing, symmetry, even and odd numbers, symbols, and other visual and non visual representations.
- Identify and use rules to generate and extend even and odd patterns.
Problem solving & inquiry concepts and outcomes
Pedagogical ideas
Activities sequence
- Groups of pairs - even, odd, multiple of three
- Groups of squares - even & odd groups of squares
- Odd & Even Beads - groups of beads
- V patterns - odd patterns
- Even & odd numbers
- Super even numbers
- Expansion ideas
Focus questions
- What is a pair?
- What kinds of groups make pairs?
- What is even?
- What is odd?
- What kinds of groups don't make pairs?
Related resources
- Conservation & assessment tasks
- Blank graph sheet
- Odd plus odd three ways : concrete, semi-concrete (iconic), abstract
- Teaching video - proof of odd + odd even concretely
Expansion activities and folow up unit
Activities
Groups of pairs
Which of the groups of pairs are odd and which are even?
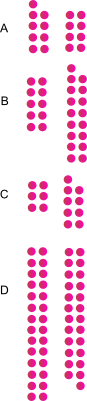
Explain how you decided which was odd and even.
Explain what convinces you that a group is even.
Explain what convinces you that a group is odd.
Odd and even squares
For each of these patterns show which are odd and even without counting.
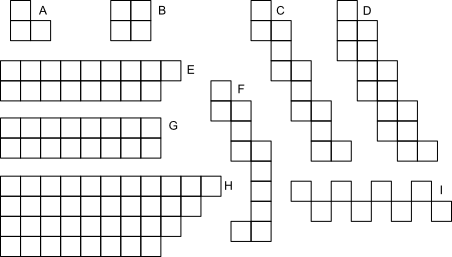
Pattern which are even:
Patterns which are odd:
How do you know?
Odd and even beads
For each group of beads show which groups are odd and even without counting.
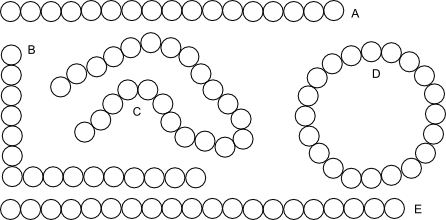
Pattern which are even:
Patterns which are odd:
How do you know?
V patterns
Below are four V patterns.

Are V patterns odd or even?
Put the number of dots in each pattern in the table.
Pattern number |
1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Number of dots |
How many dots in the next V pattern?
Can a V pattern be made with 100 dots?
How many dots in the sixth V pattern?
Numbers as even and odd
Color code numbers as even and odd.
- Start with zero and write the numbers on the path.
- Color the blocks with even numbers one color and the blocks with odd numbers a different color.

What do the different colored numbers have in common?
Think of a number not on the path.
What color would it be if it were?
Pick one of the colors you used and write a rule to describe those numbers?
What is a rule for the other numbers?
How do you know what color a larger number like 321 is?
Hint
Rules can be made with a start number, an operation, and a change number.
Start - operation - change
- 0 + 2
- (0 + 2) + 2
- (0 + 2 + 2) + 2
- (0 + 2 + 2 + 2) + 2
Super even numbers
Numbers are super even if the can be represented by even groups of pairs.
- Write even numbers on the path.
- Color perfect even numbers one color.

How many super even numbers are there less than 100? ... 1000?
Even and odd square patterns
Use the squares below to draw different shapes with different numbers of squares. Then decide if there is an even or odd number of squares in each pattern. How about all the patterns together?
