Properties of Numbers and Operations

 

Addition and Subtraction properties

Number sentence

Primary Conjecture

Property & conditions

True/False Statements

n + 0 = n When you add zero to a number you get that same number.

Identity property of addition:

For every real number n + 0 = n

  • 8 + 0 = 8
  • 7 + 3 = 11
  • 367 + 0 = 0
  • 369 + 0 = 369
  • 30 + 0 = 300
  • 2 zebras + 0 zebras = 2 zebras
  • 4z + 0 z = 4 z
  • x + 0 = 0
  • x + 0 = x
0 + n = n When you add a number to zero you get that same number.  
  • 0 + 8 = 8
  • 4 + 6 = 11
  • 0 + 763 = 0
  • 763 + 0 = 763
  • 0 + 30 = 300
  • 0 + 2 turtles = 2 turtles
  • 0T + 3T = 3 T
  • 0 + x = 0
  • X + 0 = 0
  • x + 0 = x
n − 0 = n When you subract zero from a number you get that same number.

Identity property of subtraction:

For every real number n − 0 = n

  • 8 − 0 = 8
  • 7 − 3 = 10
  • 367 − 0 = 0
  • 369 − 0 = 369
  • 30 − 0 = 3
  • 2 zebras − 0 zebras = 2 zebras
  • 4z − 0 z = 4 z
  • x − 0 = 0
  • x − 0 = x
n − n = n When you subract a number from itself you get zero.

Inverse property of addition:

For every real number n, there is a real number − n such that n + (− n) = 0

  • 3 − 3 = 0
  • 3 − 2 = 0
  • 8 − 8 = 0
  • 2 trees − 2 trees = 0
  • 2t − 2t = 0
  • b − b = 0
  • 9 − b = 0
  • 29 − n = 0
  • n − b = 0

 

Multiplication and Division properties

Number sentence

Primary Conjecture

Property & conditions

True/False Statements

n × 1 = a When you multiply a number times 1 you get that same number.

Identity property of multiplication:

For all real numbers a, a × 1 = a

3 × 1 = 3
1 × n = n When you multiply 1 times a number, you get that number.   1 × 4 = 4
n ÷ 1 = n When you divide a number by 1, you get that number.   5 ÷ 1 = 5
n ÷ n = 1, n ≠ 0 When you divide a number by itself you get one, except when the number is zero.   6 ÷ 6 = 1
n × 1/n = 1  

Inverse property of multiplication:

For every real number n, n ≠ 0, there is a real number 1/n such that n × 1/n = 1

3 × 1/3 = 1

 

Multiplication and Division with zero

Number sentence Primary Conjecture Property & conditions True/False Statements
n × 0 = 0
When you multiply a number times zero, you get zero. Property of zero 2 × 0 = 0
0 × n = 0 When you multiply a zero times a number, you get zero.   0 × 3 = 0

0 ÷ n = 0,

a ≠ 0

When you divide zero by any number except zero you get zero.   0 ÷ 0 = 0

 

Commutative property for addition and multiplication

Number sentence Primary Conjecture Property & conditions True/False Statements
a + b = b + a When you add two numbers, you can change the order of the numbers you add, and you wlll get the same answer.

Commutative property of addition:

the order in which a pair of addends is added does not affect the sum.

For all real numbers a and b,
a + b = b + a

4 + 3 = 3 + 4

1 + (2 + 3) =
1 + (3 + 2)

 
a × b = b × a When you multiply two numbers, you can change the order of the numbers you multiply, and you will get the same answer.

Commutative property of multiplication:

the order in which a pair of factors is multiplied does not affect the product.

For all real numbers a and b,
a × b = b × a

2 × 3 = 3 × 2

2 (3 × 4) = 2(4 × 3)

 
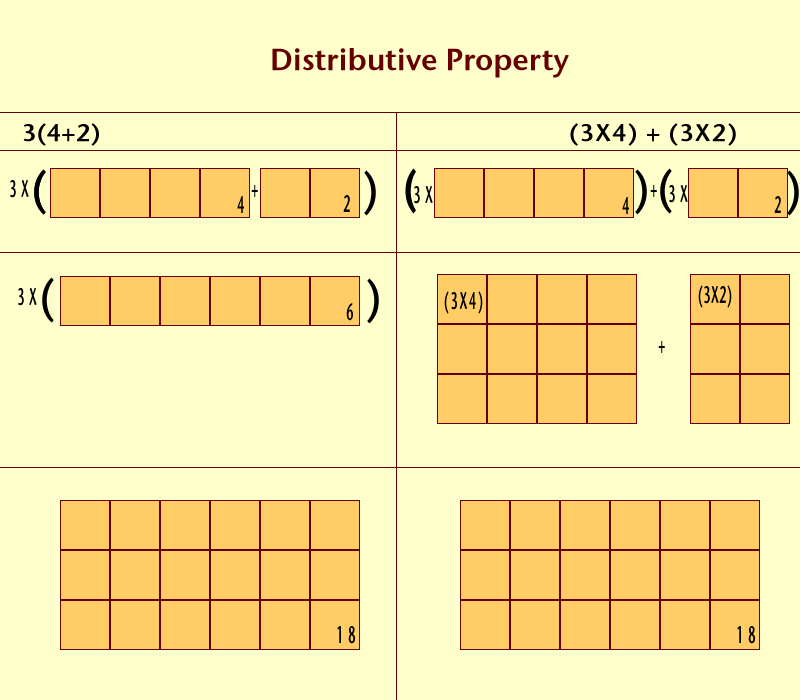
a × (b + c) =
(a × b) + (a × b) 		 

Distributive property of multiplication over addition:

For all real numbers a, b, c,
a × (b + c) = (a × b) + (a × b)

2(3 × 4) =
(2 × 3) + (2 × 4)
a + (b + c) = (a + b) + c You can add numbers in any order

Associative property of addition:

the sum of three or more numbers is the same regardless of how the numbers are grouped (use parentheses) or are added.

(2 + 3) + 4 = 2 + (3 + 4),

(25 + 2) + 8 = 25 + (2 + 8),

(10 + 5) + 12 = 10 + (5 + 12)
a × (b × c) = (a × b) × c You can multiply numbers in any order

Associative property of multiplication:

the product of three or more numbers is the same regardless of how the numbers are grouped (use parentheses) or are multiplied

(2 × 3) × 4 = 2 × (3 × 4),

(25 × 2) × 4 = 25 × (2 × 6),

(10 × 5) × 11 = 10 × (5 × 11)

 

 

Dr. Robert Sweetland's notes
[Home: thehob.net & homeofbob.com ]