Exploration of function with a variable factor and constant factor
Introduction
This page explores functions, their definitions, representations, and examples. Also includes an example function activity with a variable factor and constant factor for casting out nines.
Definitions
A function is defined as:
- a relation between a set of inputs and a set of permissible outputs such that each input is related to exactly one output.
- a rule that gives value of a dependent variable that corresponds to specified values of one or more independent variables.
Examples
Function is a relationship such that each possible input value leads to only one output value.
This means:
- The output is a function of the input values.
- The input values, make the domain.
- The output values, make the range.
Diagrams
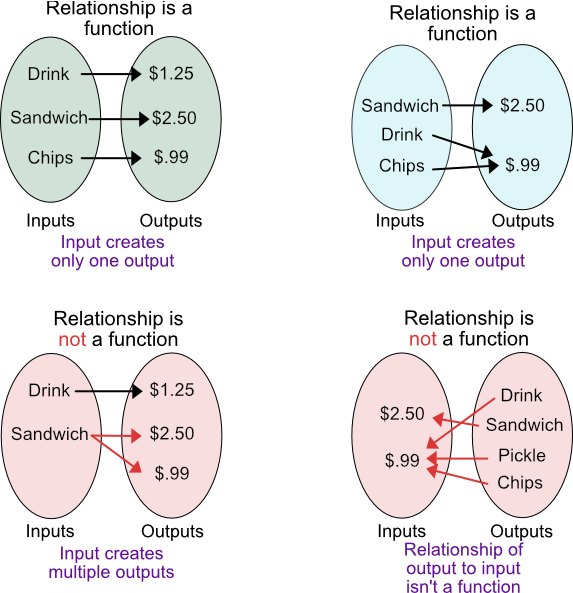
Summary:
Items on a restaurant menu have only one price. Meaning:
- Price is a function of the kind of item on the restaurant menu.
- Each item (input value) has exactly one price (output value).
- There can be items with similar prices.
- The kind of item isn’t a function of the price.
- There can be different items that have the same price, therefore the kind if item is not a function price.
Another:
Height is a function of age.
- Height is a function of .
- Age (input value) has exactly one
- There can be ages with similar
- Age isn’t a function of
- There can be different ages that have the same _______________, therefore the _________________ is not a function price.
Hints:
If you pick a unit of years for age, then height will change every year until maturity. Then each year could have the same height, but each year would have only one height.
If you use day for age, then height may not change most days, but each day would have only one height, depending on what time of day the measurement is taken.
Create ones of your own.
Class grades are a function of points earned.
Use as an example to write ….
Representations of function
Funtion machine
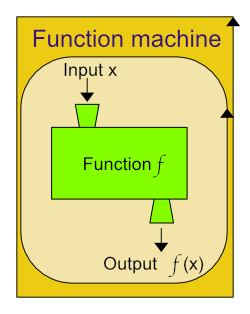
Notation
Examples
f(x) = 2x
- f tells the name of the function;
- (x) tells x is the input;
- 2x tells what the function does;
- output is the value that results from the action on the input 2 * x.
f(x) = sin(x2 + 1)
- f tells the name of the function;
- (x) tells x is the input;
- the function f takes a real number as input, squares it, then adds 1 to the result, then takes the sine of the result, and returns the final result as the output.
Sometimes the symbol f and the () are omitted and replaced by several characters.
For example, sin x instead of sin(x).
Table
A function can be represented as a table of values.
The domain of a finite function can be specified in a table.
Example, the multiplication function
f : { 1 , … , 5 } 2 → R
Defined as f(x, y) = xy and can be represented with the familiar addition and multiplication tables.
Bar chart
Bar charts can be used to represent a function of a set of finite natural numbers, or the integers.
An element (x) of the domain is represented on the x-axis as intervals of intergers (1, 2, 3, ... n). Each corresponding value of the function, f(x), is represented by a rectangle whose base is the interval corresponding to x and whose height is f(x) ( -n, ... -2 , -1, 0, 1, 2, ... n).
Exploration of a function with a variable factor and constant factor
f(x) = 27x
Domain = (3, 6, 9, 12, 15, ... 36); Range = (calculate and add to the table)
Use a electronic device to explore this function:
| Row number | Variable factor input | Constant factor | Product output |
Notes - patterns! |
|---|---|---|---|---|
| 1 | 3 * | 27 = | ||
| 2 | 6 * | 27 = | ||
| 3 | 9 * | 27 = | ||
| 4 | 12 * | 27 = | ||
| 5 | 15 * | 27 = | ||
| 6 | 18 * | 27 = | ||
| 7 | 21 * | 27 = | ||
| 8 | 24 * | 27 = | ||
| 9 | 27 * | 27 = | ||
| 10 | 30 * | 27 = | ||
| 11 | 33 * | 27 = | ||
| 12 | 36 * | 27 = |
- Find the products of the factors and enter them in the column.
- What patterns can be found?
- Write some notes about what was found.
- Did you include a pattern for the ones' place?
- Did you include a pattern for the ten's place?
- Did you include a pattern for all the places?
- Did you think to add the digits and see if that made a pattern?
- Did you think to add the digits and add the digits again until there was only one digit?
- Did you try to rearrange the digits for each product and see if that made a difference as to what it was divisible by?
- Research how this is related to casting out nines?
Hints
| Row number | Variable factor | Constant factor | Product | Notes |
|---|---|---|---|---|
| 1 | 3 * | 27 = | 81 | |
| 2 | 6 * | 27 = | 162 | |
| 3 | 9 * | 27 = | 243 | |
| 4 | 12 * | 27 = | 324 | |
| 5 | 15 * | 27 = | 405 | |
| 6 | 18 * | 27 = | 486 | |
| 7 | 21 * | 27 = | 567 | |
| 8 | 24 * | 27 = | 648 | |
| 9 | 27 * | 27 = | 729 | |
| 10 | 30 * | 27 = | 810 | |
| 11 | 33 * | 27 = | 891 | |
| 12 | 36 * | 27 = | 972 |