Memorizing basic facts & algorithms
Memory: learning basic facts & algorithms - getting learners to slow down & think how to proceed
Page Overview:
- Introduction
- Penny diagram
- Development of addition & subtraction facts
- Dot plates
- Getting learners to stop, think, & contemplate how to proceed - suggestions & activities
- Development of multiplication facts
- Multiplication table for multiples, factors, & common denominators
- Bringing it all together fact tables (matrices)
- Addition fact table
- Multiplication fact tables
When learners memorize basic facts, they are many times robbed of the opportunity to learn important mathematical relationships.
Introduction
This page discusses memory and memorization, specifically related to remembering basic facts of mathematics. Suggestions on how memory works, how it can be enhanced, how to help learners memorize addition, subtraction, and multiplication facts. It also discusses the importance of getting learners to stop, think, and contemplate; when they approach mathematical situations, beginning with counting.

Memory and memorization
We think of memory as a place where information is stored and memorization as the process of committing information to memory: learn by heart, putting something into an isolated box.
However, it doesn't always work that way.
In order for basic facts to be known, in a fashion that can be accessed within a short period of time, each fact must move from short term memory to long term memory.
Instructional strategies, like parroting facts, doesn't get information from short term memory into long term memory. To move information into long term memory the event must be meaningful or memorable and there has to be something in long term memory to which the information can connect.
The learner must be conscious of something. Something they notice and really think about. This starts in short term memory, which is limited by the amount of information to think about at one time (mental power). With enough concentration it may be possible the information is put into long term by organizing and associating it with other information. The more connections during this organization, the easier it will be to retrieve, be remembered, and retained. This is why I often tell learners, they need to learn more to remember less.
Research now suggests long term memory has to be reconstructed from time to time. Our brain has to rebuild memories or lose them. So these associations are important. Too often we forget these necessary conditions, or act as if it isn't important when we choose an activity without much thought about all the previous experiences a learner might have had. Learning in school isn't equal, even when learners are involved in exactly the same experiences.
There are many different ways people commit something to long term memory. All of them require a very memorable experience and a high degree of association to consciously connect a new idea to a previously learned idea or better yet, ideas. Learning more to remember less.
How does the type of experience learners have provide these needs?
Do we select the experiences to be powerful enough (collapse of the World Trade Buildings) or meaningfully connected enough, to assist different people to remember. Repetition alone doesn't work to guarantee remembering. More on that later.
There are a variety of different ways to remember, and some work better for some of us, and others work better for others of us. Too often we don't employ a variety of methods to make memorization of basic facts accessible to all learners. I don't mean just the teachers who teach at a grade level where the curriculum identifies a particular set of facts to be mastered. Teachers before those levels can help learners experience numerous activities early in a learner's education, that will position learners better to learn the basic facts as they develop number sense. Experiences so rich, learners will discover they know them, when they are required to know them.
Story ...
One of my sons was in third grade where the curriculum called for all learners to memorize all the basic facts of multiplication.
At a parent teacher conference the teacher proceeded to tell us how proud she was that our son was the only one who had learned the seven - multiplication facts and obviously before anyone in the class.
Being the proud parents we are, we certainly didn't want to burst her bubble and I would certainly want to give my son credit, that he was able to transfer his outside recreational experiences into the classroom.
The truth of the matter being. He loved football and has played it since before preschool.
When he played everyone who scored a touchdown got seven points. Extra points were automatic. So he knew all the touchdown multiples well before third grade.
He also learned that multiplication can be related through repeated addition, so that he could use skip counting, which he did in an efficient fashion that anyone, who didn't know, would have thought that he had committed them to memory. Which he did, first for the lower ones, later for more familiar ones, and eventually for all.
Because of the importance placed on basic facts and operations, there wasn't much depth. Five touchdowns was 35 points and so forth. He didn't have a very deep structure for these basic facts or what multiplication was other than repeated addition. However, in this class that wasn't what was most important.
Well, enough for now.
As I promised earlier: Repetition is important, but repeating without conscious practice doesn't help us remember?
As promised, here is an example:
How many times have you looked at a penny?
A few times, I imagine.
Probably more than the number of times you have thought of 8 + 7 or 8 × 7.
So which penny, in the drawings below, is an accurate representation of a penny?
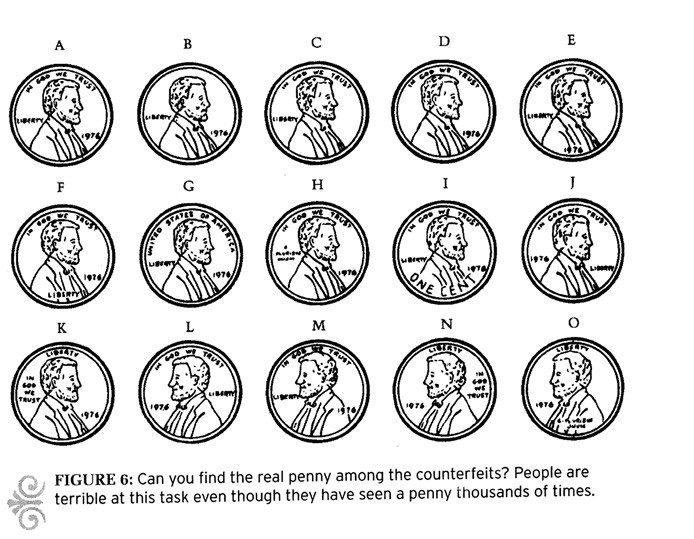
Most people can't identify the accurate representation, and the older we are the more repetitions of seeing one we have had. Experiences without conscious practice.
Remembering something isn't easy: it takes effort and connections to other information.
Learn more to remember less!
Development of addition and subtraction facts
Children add and subtract, based on their understanding of number values. They compose and decompose numbers and to build their knowledge of addition basic facts. Beginning with plus one, plus two, skip counting, counting on, and other patterns such as the commutative property. All of these are possible if learners have had a wealth of mathematical experiences.
These different patterns can be reinforced with number strips, dot lines, hundred charts, and addition tables. For example learners can use addition tables and color code the diagonal values which are commutative (2 × 1, 1 × 2; 3 × 2, 2 × 3; 4 × 3, 3 × 4; ...) to help them learn their facts.
I know schools where students do not spend considerable time drilling and practicing basic facts with flash cards, because they learn them with many powerful experiences of mathematizing number values.
So my recommendation: assist learners in learning the basic facts by beginning with many of the activities identified in the number value section. Many are memorable and if they are used and we consistently ask how they can remember a new one, they will personalize it, relate it to what they already know and have a better chance of remembering. Additionally if learners share their ideas or strategies, others will grab on to the ones that fit with their experiences and help them remember.
Dot plates
Activities such as dot plates video (thanks Brook) with 0-5 or 0-10 dots on them to flash a look and then turn them back around.
Research notes:
How does this help?
There are several things that make this activity powerful.
First, there is research that humans can know numbers in two ways. The first way is we recognize the values - 0, 1, 2, and maybe 3 just by looking at them (subitize). Not counting. Also there are visual patterns we have memorized and instantly recognize, like patterns on a die, triangle, square, die, dominoes, stars, and more.
The research also suggests that some animals can also do this. So when we flash the plates people see them as different combinations of 1, 2, and 3 and will compose them to make larger values as necessary. This composition is the second way we recognize numbers to create a number system.
How can we be sure?
Two ways.
First, it is amazing that when they stick people into an imaging machine (fmri) and do a brain scan when thinking of numbers, they see scans of people who are using two completely different parts of the brain. One part to recognize the smaller numbers and another to recognize the larger numbers. The smaller numbers are recognized in an area closer to the brain stem and larger numbers in an area more toward the frontal lobe.
Interesting ...
The second way, was discovered by people who study the historical development of language. They found that when you look back in time to see when words were first introduced into a particular language, the number words used in the earliest times had words for only the values of one, two, and sometimes three. Every other number value was referred to by something that meant - many. It wasn't until their culture invented a number system that they developed numbers for larger numbers. Interesting very interesting. See how the number of number words used to represent numbers in the English language change.
Back to the dot plates. When learners get good at recognizing the number values, you can tell them you will flash a plate and before they tell you the answer, you will tell them if you want them to tell you the number of dots on the plate or one more. Later you can do one more and one less, and even later two more or two less, and later five more, five less, and later ten ... Got the picture? I presume you do!
So dot plates assist learner's learning number value, addition facts, and subtraction.
Getting learners to stop, think, and contemplate how to proceed
Another thing I think is very powerful is when learners look at the plate, they stop and consider different ways of arriving at an answer, and none of them is counting. Because when you flash it, they don't have enough time to count.
This is important for two reasons.
- Getting young children to stop and say I can think of different ways to solve a problem - is an incredible landmark to achieve. I can't emphasize this enough. One of the most important things to learn is to stop, survey the problem, and say I can solve this a number of ways, which way should I try first?
- It is important to discourage counting. The worst thing we can do is turn learners into habitual counters. If we do, it will be the only way they want to solve problems. They will be expert counters and lousy problem solvers. Once children learn to count, they should be encouraged to solve problems any other way but counting. When I see someone that knows how to count trying to solve a problem counting, I usually put my hand over what they are counting and say. I am sure you can think of another way. Maybe count by twos or group by five's, or ....
More activities to encourage stop and thing
- How many squares? - find how many squares (or Find a counting shortcut) without counting and share how you know!
- Short cut counting - find how many circles in a pattern, then group and color your solution.
- How many toothpicks? - find how many toothpicks without counting and share how you know!
- Discuss: How I stop the counting compulsion! How I contemplate before I calculate!
- Solve this problem with mental math: 81 - 72 + 63 - 54 + 45 - 36 + 27 - 18 + 9
Hint: think 9's! or Think 90's!
More activities to support number value
Development of multiplication and division facts
Learners build off of their knowledge of addition basic facts to compose and decompose multiplication and division facts. Such as: skip counting, rearranging numbers, multiples of ten, arrays, combinations, and other patterns if they have had a wealth of these experiences in their previous experiences.
One example, used to introduce multiplication is something I see regularly in classrooms. A wall with charts for things that come in multiples:
- 0 - pink elephants in the room
- 1 - unicycle wheels
- 2 - bicycle wheels
- 3 - tricycle wheels
- 4 - car wheels
These patterns learners will use to represent and generate multiplication facts.
When students reach the level to work on their memorization of multiplication facts, a strategy I have had success using, is to display all multiplication facts on a table (12 x 12) and going through each fact and discuss how each can be remembered.
First, go through and have learners identify strategies they use to recall fact they know in the table. After learners present their strategies, you can supplement them with others, either after each fact or by going through a second time to suggest ones they may not have identified.
- Ask. How can you remember the zero facts? 0 x 0, 0 x 1, 0 x 2, ...
- 0 x anything is 0,
- Ask. How can you remember the one facts?
- 1's - 1 x anything is anything, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 …
- Ask. How can you remember the two facts?
- 2's - doubles - add the number to itself, 0, 2, 4, 6, 8 … 3's - skip counting,
- Ask. How can you remember the three facts?
- end in 0, 3, 6, 9, 2, 5, 8, 1, 4, 7, 0, …
- Ask. How can you remember the four facts?
- They are double doubles,
- Ask. How can you remember the five facts?
- They all end in 5's - multiples of five, use the clock to count fives, end in 0, 5,
- Ask. How can you remember the six facts?
- They are double threes, end in 6, 2, 8, 4, 0
- Ask. How can you remember the seven facts?
- Discuss possible ways, such as touchdowns, or tricks to memorize larger factors and products, as there are no really easy ways.
- Ask. How can you remember the eight facts?
- Discuss possible ways, skip counting for lower products and some tricks to memorize larger factors and products, as there are no really easy ways.
- Ask. How can you remember the nine facts?
- Use your fingers. Manipulate your fingers by folding down a finger between fingers to represent the smaller factor on the left, larger factor on the right. Example 2 × 9; hold hands palms out, fold down second finger from the left (ring finger) 2. You should see one raised finger (10) to the left of the folded second finger and eight fingers to the right of the folded finger (8) together they represent 18; 3 × 9 third finger from left folded with two fingers raised to the left of it to represent 20 and seven to the right to represent 7 or 3 × 9; 27.
- If you study the products for the nine facts you will see they all add to nine and the first digit Therefore, the product of digits add to nine and first digit is one less than the first factor; 4 (first digit) × 9 (second digit); 4 - 1 = 3 (first digit); then if both digits (3 + 6) add to 9, then 3 + 6; makes 36 or 4 × 9
- Ask. How can you remember the ten facts?
- Just add zero to the non ten factor
- skip count by tens
- All end in 0
- Ask. How can you remember the eleven facts?
- double digits, 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121
- Ask. How can you remember the twelve facts?
- inches in feet, 0, 12, 24, 36, 48, 60, 72, 84, 96, 108
- try 3 × 12;
- 3(first factor) x 12 (second factor)
- First digit is same as first factor 3 and last is first factor times second (3 x 6),
- works until 10 X 12.
Have learners create a chart with all the facts 12x12 matrix. Then have them cross out the facts they really know.
The purpose is to have learners identify the facts they know and how they can remember them, cross them off their personal chart, and identify the facts they will need to put more time in learning. Most learners will discover they know more facts than they initially thought and there are less than they thought that they have to develop strategies to recall.
Other ways to help arrive at basic facts.
- Use the commutative property to make easier problems 8 × 6 ? ; think 6 × 8
- Color code the diagonal values which are commutative (2 × 1, 1 × 2; 3 × 2, 2 × 3; 4 × 3, 3 × 4; ...)
- Use fact families. 6 × 8; 8 × 6; 48 / 6; 48 / 8
- 6 × 8; 48 can be thought of as 5 × 8; 40
plus 8 more; 48
- or 6 × 8; 48 can be thought of as 5 × 8; 40 plus 8 more; 48
Most learners will only have 5-15 left. The next step is to convince them that learning the few left is a manageable task. The key is to select a strategy to help recall each fact on their don't know or demon list to use to determine an answer. Get a commitment for them to identify a strategy and practice it so they can remember to use it next time. Then provide time periodically for students to review their list of strategies during practice time (drill and practice with their demon lists) until they are comfortable with all facts.
Multiplication table for multiples, factors, and common denominators
A multiplication fact table can be explored to find multiples, factors, and common denominators. At first learners may search randomly, but as they become more familiar with these relationships they will begin to proceduralize a process to find what they are seeking more efficiently.
Problems with sample scenario:
- Let's use the multiplication table to discover a procedure to find factors.
- Find the factors of six. 1, 2, 3, 6
- Share different ways they used the table
- Select a procedure and try it to ...
- Find the factors of 18. 1, 2, 3, 6, 9
- Did it work? Discuss and if need to do more then continue till ready to find common factors.
- Let's see how you can use it or expand it to find common factors.
- What are the common factors for 6 & 18? 1, 3, 6
- Share how the procedure is modified and select one to try on some more problems.
- 12 & 18
- 18, 24
- Let's use the multiplication table to discover a procedure to find multiples.
- Find the first seven multiples of six. 0, 6, 12, 18, 24, 30
- Find the first seven multiples of three 0, 3, 6, 9, 12, 15, 18
- What are multiples are common 0, 6, 12, 18
- Let's use the multiplication table to discover a procedure to find common denominators.
- What is a procedure to use the table to find multiples?
- What procedure would be used to find common multiples?
How are common multiples and common denominators related? - What are multiples of 2 & 3
- What are multiples of 3 & 6
- How can you use these to find common denominators for 2 & 3?
- Try others
used to find common factors. reduce by finding the common factors. Students explained procedurally find number in table and then look to see what numbers are left and up and use them for common multiples or factors to reduce. Ask learners to explain if it will always work and how they know that they are sure. Multiplication table is a list of multiples and factors for 1-10 or whatever. If you can find numbers in the same column or row, then they have a common factor. E.g. 21/28 both are in the row or column with 7 (3 × 7 , 4 × 7). If you take two numbers that you want to find a common multiple and find one on the side and the other at the top, you will a common multiple at the intersection. When you multiple two numbers the product will always be a common multiple of the factors, but not necessarily the least common multiple.
Bringing it all together fact tables (matrices)
When I was young I was encouraged to memorize the basic facts. I had fact tables that were only to be used to study for the purpose of memorizing. It was not acceptable to use them during actual math class. For me the task was to memorize each fact as a separate piece of information. I never thought that I could memorize and visualize the whole fact table or study the patterns in a table (matrix).
Years later, when talking with my Uncle, about how people learn math. I was struck with his statement that he learned the basic facts with a table and could visualize it. My initial response for what he achieved was based on the idea that a person could close their eyes and see a whole table in their mind's eye, as I believed required a special ability, something like a photographic memory. Therefore, I dismissed the idea that it would be reasonable for everyone to be able to visualize a basic fact table. However, I neglected to ask additional questions to explore more about how he visualized his tables. ☹
Years later, when exploring the basic fact tables for patterns, I realized it possible to visualize part of a fact table and construct the areas around it. With practice the number of cells visualized can be increased. For example: visualize, or begin by actually looking at a table to construct the patterns you need to use. So visualize or find on an addition table a three and two on the edges of and their intersection at five, then imagine a four before the five, a six after it (left, right), because the values increase and decrease by one as you move right and left or up and down, it is easy to imagine these values.
Close your eyes and see them in your mind's eye. Then, similarly, visualize the four above it and six below it. Then visualize the four diagonal numbers that is the sum.
This is a bit more tricky than one more or less for the horizontal numbers. Two of the diagonal numbers being one and two more and one and two less, with the other two being equal to five, relative to the five.
Depending on where you focus you can visualize the eight numbers around the five and relate them to the corresponding addends on the edges of the table. As you chunk numbers together, you can visualize more numbers simultaneously. However, my visualization is limited to a focus of about eight numbers at best. I don't know if that is a working memory limit or with more practice and chunking it could be expanded. For my uncle it was possible for him to visualize the whole table and discover the sums for all.
Okay, you say, you have to know all that information so you can't use the process to find facts you don't know. Ah! maybe not. ☺ Let's say I want to look up 6 + 8.
I know a landmark or double double: 6 + 6 is 12 so I can visualize that in my mental table. I can see 12 and know 8 is 2 more to the right of 6 so I move two right past 13 to 14. Similar adjustments can be made for all eight directions around a landmark number.
While learners may not want to visualize a fact table the exploration and discussion of different patterns helps to see hierarchical inclusion, different ways to decompose and compose numbers, and can be an introduction to matrices, functions, and other patterns (algebra) to develop a better number sense and begin to understand how relationships can be represented in matrices and relate to basic facts.
Yes, it is the same as decomposing 6 + 8 to 6 + 6 and composing 12 + 2 or subtracting two and adding two and maybe other strategies. So if that works better for you, then have at it. However, I think it is kind of cool as a mental exercise to be able to visualize part of the table. Yes, for me it takes a lot of mental power to just see a small part of the table, but the more I work at it, the better I can construct different parts at a time. Like looking through a microscope and seeing part of the specimen you are looking at as you move it around. However, that is my view, others may be able to create a larger field of view. Give it try.
I have used the same process for the multiplication table. Only it is a bigger challenge, as the numbers in rows and columns increase and decrease as multiples. However, knowing multiples or being able to skip count makes it achievable. Go for it and see how it works for you. ☺
Addition facts 9 X 9 table
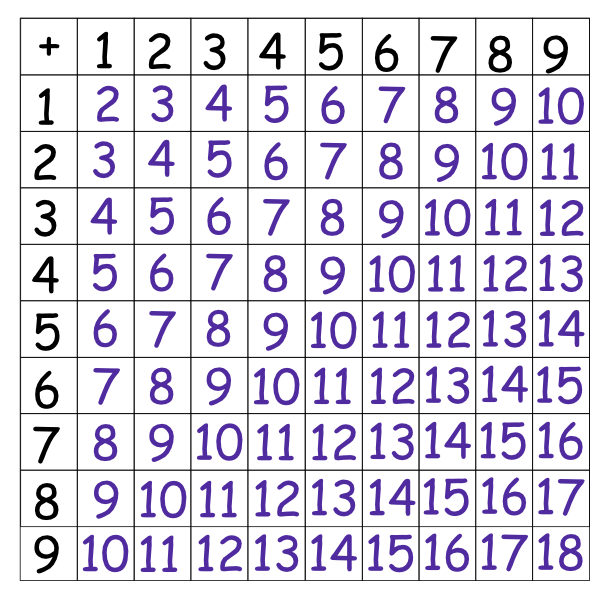
Multiplication facts 9 X 9 table

Multiplication facts 12 X 12 table

How many squares?
Directions:
Use patterns to find how many squares there are.
No counting! or Find a counting shortcut!

Short cut counting
Directions:
Use patterns to find how many circles there are.
Find a counting shortcut! or No counting!

Use the dots below to group and color how you figured how many circles!

Additional references
- Cognitive development of reasoning and conservation,
- Development from infant to adult - an outline that includes visualization for movement, exploration, & reasoning
- See als0 Play in Learning & human development
- Logic, reasoning, and proof,
- Number value
- Representation in mathematics
- Representation concepts related to math and sciences in Mathematical Knowledge base