Problem solving
Developing mathematical problem solving
Questioning is the foundation of all learning.
The first step in rejecting not knowing is to ask, why?
Sweetland

Introduction
Page Overview:
- Introduction
- Heuristic:
- Strategies for solving problems with sample problems
- Planning & teaching tools pedagogical and curriculum
- Problem solving environment - atmosphere
- Teacher's role in problem solving
- Suggestions to help learners solve problems
- Assessment sample questions to assess learners' mathematical problem solving
- Characteristics of a good problem ideas to consider when writing or selecting problems
- Planning questions to prepare to facilitate problem solving & investigating suggestions to consider when writing or planning to use problems
- Problem Solving Goals and Outcomes to review for the inclusion in appropriate curricular documents and plans
- Knowledge base with concepts, misconceptions, outcomes, standards
- Problem solving vocabulary to introduce to learners
- Dispositions to review & select to focus on
- Learner's materials
- Learners problem solving guide or checklist to use to as a guide with suggestions to solve problems
- Learners solving checklist - with before, during, and after suggestions
- Learners Solving Attitude Inventory with yes - no questions
- Reflect on the quality of these questions
Good problem solvers have a general procedure (heuristic), and a repertoire of strategies to use along with metacognition and a positive problem solving disposition to engage successfully in problem solving.
This page includes information to assist in a reflection of how to become a better problem solver and to facilitate problem solving with others.
Background
In 1945 George Polya published his classical book: How to Solve It. In it he identifies a heuristic to use to systematically solve problems, which has been been found, by students and educators, as a powerful tool for solving problems. In it he suggests a four step heuristic for solving problems:

- Understand the problem
- Make a plan
- Carry out the plan
- Look back on your work and ask, How could it be better?
In his book he describes these steps and ideas to expand them and how to proceed if the problem still doesn't seem solvable. How to Solve It summary. Or Book in .pdf
Information on this page builds on his ideas and provides information to help educators and parents who want to explore problem solving for themself or to facilitate learners in their abilities to solve problems.
This information is organized around characteristics of what good problem solvers do: use a heuristic (general procedure), have a repertoire of strategies, use metacognition and develop a positive problem solving disposition.
Additionally, educators and parents can encourage problem solving by providing a problem solving environment and challenging problems from time to time.
To assist with this, ideas and tools with suggestions for planning and teaching problem solving, to create curriculum materials, mathematical problems, and suggestions on how to facilitate learners in becoming good problem solvers to attain mathematical literacy. are included.
Heuristic
A heuristic is a series of general steps which are helpful to know when solving problems. When you use a heuristic it helps you think about what you know or have done and what you need to find out or do to solve problems.
Any one who attempts a problem uses some sort of heuristic. A good question to ask is: how detailed should it be?
To seek an answer to this question, let's look at three levels of possible detail.
A simple beginners heuristic has two steps: meet a problem, try a strategy (usually an operation + - * /).
A step up is the four step heuristic, of George Polya.
To make it more comprehensive, one idea is to add more steps, like the eight step heuristic below.
However, the more steps added, for comprehensiveness, the harder it becomes to remember all the steps. To help us remember, a good way is to keep the steps small and chunk ideas with each step. For example: four step heuristic with subcategory chunks.
I usually begin each year giving students a problem to solve. One I really like is the forty square puzzle. Then, after solving it, we would review what they did, to solve it, and make an initial heuristic.
The following three heuristics are examples created by different levels of students.
Four Step Problem Solving Heuristic
- Understand the problem
- Make a plan
- Try the plan
- Look at the solution
Eight Step Problem Solving Heuristic
- Use a problem solving mind set
- Understand the problem and state it in my words
- Identify important information
- Identify strategies that might solve the problem
- Can I solve the problem?
- Try a strategy
- Check the outcome
- Can the problem be solved another way?
Problem Solving Heuristic
1. Understand the problem
- Engage a problem solving mindset
- Communicate the problem in multiple ways
2. Plan
- Review what is known
- Decide if more information is needed.
- Review possible strategies
- Identify a likely plan
3. Try a plan
4. Reflect to verify and improve
- Examine the solution
- Try another strategy
- Examine plans, process, and mindset
The initial heuristic learners create, at the first of the year, doesn't need to be comprehensive. As they solve more problems through out the year, you can review the process used to solve problems, and encourage them to consider how to make the heuristic easier for them to use and more comprehensive (see below for possible additions to make it a more comprehensive).
Additionally learners might wonder how they could include different strategies used to solve different problems. To keep the heuristic streamlined as a procedure, I encourage learners to make a separate list for strategies, which is discussed next.
Problem Solving Heuristic
1. Understand the problem
- Engage a problem solving mindset
- Communicate the problem in multiple ways
2. Plan
- Review what is known
- Decide if more information is needed
- Review possible strategies
- Ask. Can I solve the problem? If not, can anyone solve the problem?
- Ask. Need research?
- Identify likely plan
3. Try a plan
- If it works, ask, is there another way to verify the solution?
- If it doesn't work review the plan and maybe select another plan
- Decide how to communicate and share solutions and process
4. Reflect
- Examine the solution
- Try another strategy
- Examine plans, process, and mindset
Strategies
To solve a problem, a strategy must be used. Young learners often believe selecting an operation to operate on the numbers is the entire process. However, a good educator can help them understand a heuristic and develop a repertoire of strategies beyond this limited vision, which will empower them to be better problem solvers and to solve complex problems.
To help learners develop their repertoire of problem solving strategies, they must have opportunities to engage with a variety of problems and recognize the strategies they use to solve them. Therefore, it is important to provide problems for different strategies, process their use, and have learners create a list of strategies to use with their heuristic. A list of strategies follows and some sample problems are included.
Strategies for solving problems with sample problems
- Use manipulatives, pictures, diagrams, notes, to represent objects and actions in the problem.
- Work it backwards
- Mazes - sample mazes created by learners
- Passengers on a bus & train problems
- Fruit fly problem
- A king one day decided to send out his knights in search of mathematical wisdom. One day the king ordered some of his Royal Guard to search throughout the kingdom for mathematical wisdom. They did not return. On the second day he sent out four more knights than he had sent out the day before. Each day the king kept sending out four more knights than he had the day before. Twenty - two knights left the castle on the fifth day. How many knights in all did the king send to look for mathematical wisdom?
- Chris was broke on Friday before she received her weekly envelop of spending money. On Friday night she spent $1.25. On Saturday her brother paid her a $1 he owed her. How much was in Chris's envelop if she now has $2.25?
- Guess and check, trial and error
- Chris and Sue saw some birds and dogs in the park. Chris said, "We saw 18 birds and dogs." Sue said, "Yes, and they had a total of 52 legs." How many birds and dogs did they see?
- Bucket problems
- Magic triangles & magic square perimeter
- Cork & bottle price - guess & check, trial & error, later algebra
- Use a graphical representation
- Organize information with writing, pictures, diagrams, maps, webs, outlines, charts, tables, lists, Venn diagrams, and dichotomous keys
- How many pockets are there in the indoor clothes of students in class?
- Mysteries as problems - Ten scenarios to making word problems approachable. I used Which witch is which on Halloween and students really enjoyed solving the problems in that mystery ... Many clue words & opportunities to draw a diagram or sketch.
- Acrobats problem diagram, proportion, & logic
- Different ways to communicate problems
- The Konigsberg bridges problem
- Six people entered a tiddlywinks tournament. Each player played each other person one time. How many games were played?
- A lizard lives inside a ten meter well. As the temperature increases each day as summer approaches the lizard crawls up the wall 5 meters. However, as it cools off at night it crawls back down 4 meters. If it does this each day in a row, how many days will it take before it gets to the top of the well?
- Roll die, dice, to find experimental probability by charting rolls. - unit plan with lab notes & fact sheets
- Mowing grass problem
- Sum of angles in pentagons
- Use a pattern, model, representation, equation, or function
- Petals around the Rose - is a simulation to find a strategy to determine the number of petals around the rose as simulated by dice. Directions & hints
- Look for a pattern, categorize, list, Venn diagram, chart, Patterns for quantity, AB/AB, ABBA/ABBA, size, area, volume, rotation, shading, shape, position, subtraction, addition, reflection, multiplication, analogy, and recursive
- The Konigsberg bridges problem
- Calender problems
- Use proportion & fractional parts to find the Area of nine shapes in a 17 square unit rectangle - The Pharaoh's problem
- How big is a million dollars -
- Use equivalent numbers 3/5, 6/10, 60/100, .6, 60%
- Strategies for additon & subtraction
- Strategies for multiplication & division
- Equality & equal arm balance
- Numerical, letters, size, rotation, shading, shape, position, subtraction, addition, reflection, multiplication, and recursive
- Solve a simpler problem or Break a problem into two related problems and solve the original problem in two steps: one for each problem.
- Use smaller numbers
- Think of a similar problem
- Look for clue words
- Mathematica language for mathematical objects, their properties, uses, and operations
- Mysteries as problems - Ten scenarios to making word problems approachable. I used Which witch is which on Halloween and students really enjoyed solving the problems in that mystery ... Many clue words & opportunities to draw a diagram or sketch.
- Make an analogy
- Process of elimination or process of identification
- Try a completely different approach
- Act it out mentally or physically
- Six people entered a tiddlywinks tournament. Each player played each other person one time. How many games were played?
- The Door Bell Rang by Pat Hutchins - a different way to share sharing 12 cookies each time after the door bell rings.
- Readers theater for a Carnival game - in a project based learning agenda for a different learning experience.
- Use logical reasoning: matrices, deductive, inductive, truth tables
- Die, dice, to find experimental probability by charting rolls and then reasoning to find theoretical probability. - unit plan with lab notes & fact sheets
- Acrobats problem diagram, proportion, & logic
- Passengers on a bus & train problems
- Petals around the Rose - is a simulation to find a strategy to determine the number of petals around the rose as simulated by dice. Direcctions & hints
- Equality & equal arm balance
- Sudoku - samples, free puzzles, hints, strategies ...
- Use algebraic reasoning
- Brainstorming
- Use a design process to create real life products or 3-d models.
Planning & teaching tools (Pedagogical and curriculum tools)
Information, so far, reviewed heuristics witht their major elements of problem solving and strategies for solving problems.
The following information includes tools to create a supportive environment, to support problem solving with: an instructional role in problem solving, suggestions to help learners solve mathematical problems, ideas to select or make problems, ideas to include in curriculum plans, instruction, assessment, and materials to use with learners.
Problem solving environment - atmosphere
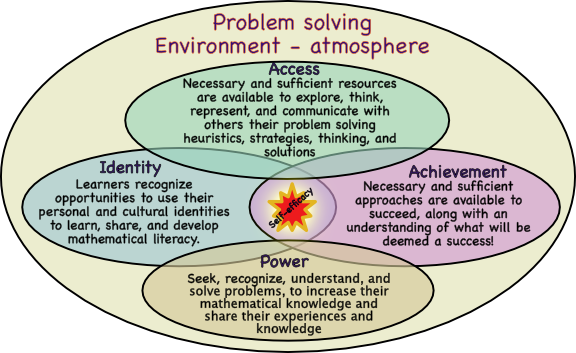
The model above represents some conditions that encourage problem solving success. This article reviews ideas on how to implement and achieve positive group and classroom environments.
Educator tools
- Teacher's role
- Suggestions to help learners solve problems
- Questions to assess learners' mathematical problem solving
- Characteristics of a good problem ideas to consider when writing or selecting problems
- Planning questions to prepare to facilitate problem solving & investigating suggestions to consider when writing or planning to use problems
- Problem Solving Goals and Outcomes to review for the inclusion in appropriate curricular documents and plans
- Knowledge base with concepts, misconceptions, outcomes, standards
- Problem solving vocabulary to introduce to learners
- Dispositions to review & select to focus on
Learners materials
- Learners problem solving guide or checklist to use to as a guide with suggestions to solve problems
- Learners solving checklist - with before, during, and after suggestions
- Learners Solving Attitude Inventory with yes - no questions
Teacher's Role in Problem Solving
- Give suggestions not answers.
- Offer a problem solving heuristic.
- Teach a variety of problem solving strategies.
- Allow time for the learners to struggle with a problem.
- Choose problems that require time to think through a solution.
- Provide a variety of problems.
- Allow learners time to practice a heuristic and strategies.
- Give similar or the same problem in different ways so learners can apply what they learned and see value in their efforts.
- Ask questions that encourage learners to:
- represent the problem.
- think divergently.
- explain how they are thinking.
- to share strategies.
- think of other ways that the same problem could be asked.
- think of real life problems that are or relate to the problem.
- discover different problems that can be solved with the same strategy
- discover multiple ways to solve the problem.
- reflect or check their solutions.
- reflect and discuss how they imagined a certain strategy might be possible.
- explain why they have confidence in their solutions.
- that really probe their depth of understanding. Don't assume.
- Provide encouragement and appreciation:
- appreciate different solutions and strategies.
- encourage learners to find multiple solutions to a problem.
- encourage learners to take time to solve problems.
- compliment students on good problem solving strategies whether they reach a solution or not.
- make sure learners know what any compliment or praise specifically relates to for solving the problem and problem solving in general.
- encourage students to keep trying and to learn by correcting mistakes.
- let students know that problem solving is difficult and rewarding.
- share and discuss attitudes and dispositions that are conducive to problem solving.
- when learners have the appearance of satisfaction, ask did you enjoy ...
- Be a role model:
- solve problems yourself.
- make problem solving a top priority.
- let students know that problem solving is an integral part of your curriculum.
- look for and comment on problem solving situations anywhere they occur.
- embed teaching and learning in a problem solving format.
- use sketches, manipulatives, charts, graphs, and any other kinds of representation that can communicate in different ways.
- Use problem solving strategies and vocabulary.
Use Metacognition, reflection, and problem solving dispositions
Metacognition (conscious thinking about ones decisions and how they affect what one is doing and has done) along with a positive disposition will not only help solve the problem at hand, but if learners recognize a purpose in studying their thinking, they will apply what they learn to create a better problem solving process and be better problem solvers.
They will not only have a problem solving process (heuristic), a repertoire of strategies to solve problems, a desire and disposition to find new problems, and develop the self-efficacy to know they are capable and can solve problems successfully.
Let's see how this problem solving can be used by educators.
Suggestions to Help Learners Solve Mathematical Problems
- Get the learners attention.
- Establish a rapport with the learners.
- Establish what the learners are thinking. Look at what they have done. Ask them what they have done. Ask them to show you what they have done. Use a heuristic to step through what has been done. Careful not to jump to any conclusions before you understand where they are in their thinking. Many times they will solve their own problems when you ask questions to find what they are thinking and wait before making suggestions. Give them the opportunity and pleasure to do as much as possible on their own.
- Focus on the problem and the strategy to solve the problem. If you must focus on the answer then say,
- What do you think about that answer?
- Can you tell how your answer makes sense for the problem?
- Does that answer look right? Vs. You got that one wrong.
- When you are fairly confident you know there is a problem and what it is, refrain from telling them what to do immediately. The long range goal is to enable them to solve their own problems. Therefore, think about how you can ask a question they might ask to help solve the problem on their own. Or model how you would solve the problem by, thinking aloud as you would step through a problem solving heuristic or select a strategy, or initiate a procedure. For example if they do not understand the directions. Say, Let me see. What do the directions say? Then read the directions aloud. Act like you really do not know and are reading them for the first time and model a strategy to understand what the problem is. Maybe to jot down ideas on the board about the problem or use manipulatives or objects to represent ideas and restate it more clearly.
- If vocabulary isn't known decide how to find out what the words mean.
- Restate the problem in your own words or act it out with manipulatives or drama.
- Use the learners' ideas whenever possible. If they have started using a strategy to solve the problem, then stick with that strategy until it works or they suggests it won't work. Avoid saying here try this way, when this way is different than what they are doing. The way you understand, may not be the way they can understand and most likely they will not use your ideas after you leave or after they complete the assignment. If the strategy, the learners have chosen does not work, then suggest a counter example and let them discover the strategy doesn't always work. The learners must decide to try a different strategy before you introduce it.
- If they reach a dead end, you can stop for the time being and let them chew on it awhile. If you feel hints are necessary, then you might suggest one by beginning with ... Here is something others have tried ... What do you think?
- Use wait-time after you ask a question and after the learners respond. If you ask them to think about a new idea use plenty of wait time. It is not unusual to wait 15 - 30 seconds. You need to look at the learners and see if they are thinking or confused. Do not allow a lot of time for them to be embarrassed. If you are listening to the them and watching their expressions you will know the difference.
- Don't stop when they have solved the problem. Ask them if they can do another problem. Or, ask if they can think of another type of problem for which they can use the strategy. If they can't make up a problem to give to them. Don't be afraid to give them a problem that will not work.
- Ask them to describe what strategy they will use to solve future problems.
- Celebrate the experience.
Questions to assess learners' mathematical problem solving
- Do they use a heuristic?
- Do they come up with strategies on their own for solving problems, or do they expect others to tell them what to do?
- What do their strategies reveal about their mathematical understanding?
- Do they understand there are different strategies for solving different kinds of problems?
- Do they articulate their strategies and try to understand other strategies?
- How do they use materials to model a mathematical situation to find solutions?
- How do they keep track of and record their work?
- Is it difficult for them to talk, draw, and write about their work?
- Do they solve mathematical problems in ways that make sense to them?
- How do they work with peers cooperatively, participate in whole class discussion, and share ideas, materials, and their creations?
- Do they learn from the thinking of others?
- How do they work independently?
- Do they have confidence in their own thinking?
- When given choices, what do they choose: a situation similar to a previous one or a different one?
- Do they stay in one place, occasionally move comfortably, or move around a lot?
- Do they consider their disposition when attempting to solve problems?
- Do they keep a record of problem solving strategies?
- Do they use metacognition when solving problems?
Characteristics of a Good Mathematical Problem
1. Interesting - As a topic, subject, or includes people or characters that are interesting. It is fascinating enough to create curiosity and develop a need for a solution. It requires some kind of action to solve - physical manipulation, observation, measurement, classification, or arranging a pattern. Something to entice learners to get involved and focus their attention to bring enough information into their working memory for an initial internal representation that has a chance to lead to a successful solution.
2. Time - The amount of time required to solve the problem is appropriate for the learner's developmental level.
3. Developmentally appropriate - The problem can be solved in a way that will not contradict the learner's developmental way of understanding, if the learner isn't ready for a developmental change.
4. Understandable - Has at least one solution that can be understood by the learner. A solution which is understandable with the mental structures available to the learners so they can organize the information, create an accurate representation of the problem, and operate on it in a manner necessary to solve the problem.
5. Emotional value - The problem has characteristics that make it reasonable to assume learners have sufficient self-efficacy and self-confidence to attempt the problem and persist long enough to solve it so they will grow to appreciate and value mathematics in their lives.
6. Communication - The problem provides students with a need or desire to communicate multiple ideas and in multiple ways.
7. Mathematical value - The problem requires mathematical ideas that are powerful and something the learners should know at this point in their lives, will be able to apply it to their world to connect to other mathematical content and process knowledge to increase their feelings of empowerment by knowing.
Planning questions to prepare to facilitate problem solving & investigating
Includes UDL (Universal design for learning) guidelines
Imagine doing the investigation and answer these questions:
Questions to think about how to make it more approachable and engaging:
|
Questions to think about to make it more purposeful:
|
Questions to think about so it will accomplish the purpose for doing it.
|
Questions to think about to make it more teacher friendly.
|
Problem Solving Goals and Outcomes
Use a Heuristic
- Recognize and use a heuristic (general plan) to solve all mathematical problems.
- Create a heuristic (a generalized pattern/procedure) to solve problems.
- Identify steps to include:
- Understand the problem,
- Select and try a strategy,
- Examine the solution, and
- Verify the solution.
- Recognize and move from step to step in the process of solving a problem. For example: recognize a strategy isn't working and step back to select and try a different one. Reach a possible solution and attempt to verify the solution.
- Review their problem solving process.
Problem Solving Skills for steps in a heuristic
Understanding skills
Describe ways to aid in understanding the problem: such as identify the words in a problem that describe mathematical relationships, operations and numerical values.
- Analyze problem as familiar or unfamiliar
- Accurately communicate the problem in their own words, diagrams, or other ways to communicate.
- Identify information necessary to solve the problem.
- Identify information unnecessary to solve the problem.
- Clearly state the problem or task
Planning skills
- Identify what solution is needed
- Identify operations or other actions necessary to solve the problem
- Select a strategy or strategies to solve the problem
- Review the plan to see if it matches with the initial ideas of what information is necessary and any unnecessary
Plan implementation skills
- Solve the problem
- If the plan doesn't seem to work, check the accuracy of implementation or review the plan and strategy, or make a different plan.
Reflect to verify and improve skills
- Assess the reasonableness of a solution for a problem with respect to the information in the problem and the approaches used
- Justify solutions
- Solve problems in different ways to gain confidence in the solutions.
- Reflect on what was learned and how it might be used in other contexts. The process, the accuracy of the solution, and the mind set.
- Share the process, strategies used (successful and unsuccessful), attitudes, and solutions.
- Develop a repertoire of problem solving strategies
- Identify a variety of problem solving settings
- Extend or generalize problems
- Extent a solution or process from solving a problem with respect to the information in the problem and/or the approach used
Meta cognitive
- Monitor and reflect on the process of mathematical problem solving and regulate their actions.
- Have the habit and ability to monitor and regulate their thinking processes at each stage of the problem - solving process
- Use self talk, group discussion, to talk through a problem and problem solving process to reflect on all the decisions that are possible to better insure an accurate solution.
Disposition/attitude habits of mind
- Have self - efficacy in their ability to do mathematics and to confront unfamiliar tasks without being given a ready - made prescription for a solution
- Have a willingness to attempt unfamiliar problem
- Open-minded and skeptical
- Not easily ready to declare a solution accurate without confidence in a solution
- Have perseverance when solving problems and are not easily discouraged by initial setbacks
- Enjoy and feel a sense of personal reward while doing mathematical thinking, searching for patterns, and solving problems
Identify and Use Strategies
- Use of manipulatives to represent objects and actions in the problem.
- Work a simpler problem.
- Trial and error, guess and check.
- Work backwards
- Use smaller numbers
- Use systematic steps.
- Look for, recognize and describe patterns: quantity, AB/AB, ABBA/ABBA, size, area, volume, rotation, shading, shape, position, subtraction, addition, reflection, multiplication, analogy, and recursive
- Break a problem into two related problems and solve the original problem in two steps: one for each problem.
- Act out the problem. Physically or mentally.
- Drawing pictures or diagram to represent the problem.
- Problems can be solved with models, graphical representation, and equations.
- Categorize information (chart, table, map) to find relationships and patterns that will assist reasoning and proof.
- Organize data to look for patterns sequence, chart, table, making a graph, Venn diagrams, and dichotomous key.
- Process of elimination or process of identification
- Write an open sentence
- Use algebraic reasoning
- Use logical reasoning: matrices, deductive, inductive, truth tables
- Brainstorm, exploratory talking, make a rough draft,
- Use equivalent numbers 3/5, 6/10, 60/100, .6, 60%
Scoring guides & rubrics
Scoring Guide or Rubric for Problem Solving
Information on assessment and how to create scoring guides and rubrics.
The first two scoring guides have the same information in two different formats.
- The first is in an outline form with a narrative for each level that combines several categories within each level.
- The second has the same information in a table format with categories in separate subcategories.
Scoring guide outline in a narrative format with categories combined
- Beginning - Try to solve problems from memory. Believe solutions are known and need to be recalled or they just pop into your mind.
- Progressing - Try to solve problems from memory, but if unable to recall a procedure and strategy will seek to understand the problem and try to discover them to use to solve the problem by random search for a solution.
- Proficient - Try to solve the problem from memory, but if unable will choose a mindset to implement a heuristic or procedure that includes steps to understand the problem, restate it in their own words, seek strategies, choose and implement a strategy, and check its accuracy.
- Advanced - Try to solve the problem from memory, but if unable will choose a mindset to implement a heuristic or procedure in a systematic manner that includes steps to understand the problem, restate it in their own words, seek strategies, choose and implement a strategy, check its accuracy by trying alternative strategies to achieve equal results, communicate the process and results, and reflect on the process while solving and after.
Scoring guide: in a table with a narrative format with categories separated
| Beginning | Progressing | Proficient | Advanced | |
|---|---|---|---|---|
| Indicator | Try to solve problems from memory. Believe solutions are known and need to be recalled or they just pop into your mind. | Try to solve problems from memory, but if unable to recall a procedure and strategy will seek to understand the problem and try to discover them to use to solve the problem by random search for a solution. | Try to solve the problem from memory, but if unable will choose a mindset to implement a heuristic or procedure that includes steps to understand the problem, restate it in their own words, seek strategies, choose and implement a strategy, and check its accuracy. | Try to solve the problem from memory, but if unable will choose a mindset to implement a heuristic or procedure in a systematic manner that includes steps to understand the problem, restate it in their own words, seek strategies, choose and implement a strategy, check its accuracy by trying alternative strategies to achieve equal results, and reflects on the process while solving and after to improve on their problem solving abilities. |
Problem solving scoring guide: outlined in a narrative format
| Indicator | Beginning | Progressing | Proficient | Advanced |
|---|---|---|---|---|
| Reflects | Try to solve problems from memory. | Try to solve problems from memory and thinks about the steps taken and how to implement them and make decisions as they solve the problem. | Try to solve problems from memory and thinks about the steps and mindset to solve problems and their processes to solve them. | Try to solve problems from memory and thinks about the process while solving and after to improve on their problem solving abilities and their mindset to solve them. |
| Mindset | Attempts to solve the problem | Recognize the way they approach a problem will affect their success. | Recognize mental variables will determine their success and alter their behavior for a greater chance of being successful. | Have a mental set of variables they use to alter their behavior to support problem solving and increases the chances of success. |
| Heuristic, procedure | No set plan. | Aware that a series of steps can be followed to solve problems. | Know a comprehensive heuristic and use it in a flexible and accurate way to solve problems. | Know a comprehensive heuristic and use it in a systematic, flexible, efficient, and accurate way to solve problems. |
| Implement a strategy | Occasionally selects an appropriate strategy. | Aware of different strategies and attempts to implement one. | Aware of different strategies and use one or two to solve most problems. | Aware of multiple strategies and implements them to check their accuracy and marvel over how different strategies can achieve verification and confidence in solutions. |
| Checks or finds multiple solutions | If achieves a solution does with difficulty and satisfied with success. | Solves the problem singularly and listens when other solutions are presented. | Solves the problem in multiple ways that are similar or inverse operations, listens when other solutions are presented. | Generates multiple ways ways to solve the problem with some being unusual and not often selected as solutions, listens when other solutions are presented and offers suggestions for improvement. |
| Communicate | May be able to summarize a few highlights when asked. | Communicates results orally and in writing. | Communicates how results were achieved orally and in writing with information for the heuristic, strategies, and multiple solutions to verify them. | Communicates how results were achieved orally and in writing with information for the heuristic, strategies, multiple solutions to verify them, and how metacognition is helpful for problem solving and excited about improving their problem solving with metacognition. |
Cool Right!
General heuristic check sheet for learner actions on steps with and without prompts
| Categories | Observed without a prompt | Observed after a prompt | Unable to do without significant help |
|---|---|---|---|
| Understands the problem before selecting a strategy | |||
| Selects a strategy after reasonable contemplation | |||
| Accurately implements a strategy | |||
| Justifies results | |||
| Use a systematic approach [heuristic] (understand problem, identifies needed information, considers strategies, plan and implements a plan, solves, verify solution). | |||
| Uses appropriate dispositions - willing to try, open-minded, confident, persistent, skeptical, ... | |||
| Understands the problem beyond rote application of a procedure | |||
| Reflects and uses metacognition during the process | |||
Problem solving - with three categories (understand problem, strategy section, and accuracy) and three levels
| Category | Scores |
|---|---|
| Understanding the Problem | 6 - Complete understanding of the problem as demonstrated by an accurate representation 3 - Part of the problem misunderstood or misinterpreted in a representation 0 - Complete misunderstanding of the problem and inaccurate representation |
| Selection of a strategy | 6 - Strategy can lead to an accurate solution 4 - Strategy selected is incomplete and additional strategies need to be used to achieve a solution 3 - Strategy selected will not achieve a solution 0 - No strategy selected |
| Accurate solution | 3 - Solution is accurate, correctly labeled for the representation of the problem 2 - Copying error, computational error, for a solution within a logical range or partial solution for a problem with multiple solutions 0 - No answer, or wrong answer based on an inappropriate strategy or representation |
Student materials to assist problem solving
- Problem solving guide or checklist to use to as a guide with suggestions to solve problems
- Problem solving checklist with before, during, and after suggestions
- Problem Solving Attitude Inventory with yes - no questions
Learner's Problem Solving Guide
Name
Date
1. Is there a problem to solve? (Yes - No - Possibly)
2. What is it? Exact statement of the problem:
3. What information is needed to solve the problem?
4. Where can it be found?
5. Can I solve this problem?
(Easily - With a lot of work - No - Maybe)
(By myself - With help)
From whom
5. How long will it take me?
6. What patterns can I see in this problem?
7. What strategies might work?
8. What order should I try the strategies?
9. What would I estimate as an answer?
10. Answer these questions when you get to the half way point on your list of steps:
Are things going as planned? (Yes - No - Maybe)
Should I (Continue - Reevaluate)
11. Answer this question when the problem is solved: How did it turn out? (hints in chart)
| Very successful | Pretty successful | Unsuccessful |
|---|---|---|
| Is really finished | Could use more work | Don't know what to do next |
| Was harder than expected | Was easier then expected | Was as hard as expected |
| Took longer | Took less time | Took what I thought |
12. Can I use the solution and/or the problem solving strategies in the future? (yes no)
If so what future uses?
Problem Solving Checklist
| Before you begin to solve the problem: Did you? | ...✔... |
|---|---|
Read the problem more than once. |
|
Establish a mindset determined to solve it. |
|
Know what the problem is asking. |
|
Know what information is needed to solve the problem. |
|
Determined if you have ever experienced a problem like it before. |
|
Determined if there is unnecessary information in the problem. |
|
| During your problem solving: Did you? | ...✔... |
Look back at the problem to confirm if the selected strategy is appropriate. |
|
Stop and reflect if the procedure is being used completely and accurately. |
|
Check each step of the procedure is being done accurately. |
|
Consider starting over and do it differently. |
|
Determine if what you are doing is getting you closer to an answer. |
|
| After you finished solving the problem: Did you? | ...✔... |
Checked to see if the calculations are correct. |
|
Reflected on it the strategy used and ask if it you still think it is appropriate for the problem. |
|
Looked at the answer and asked if it made sense for the problem. |
|
Think about a different way to solve the problem. |
|
Solve the problem with a different strategy. |
|
Tried to discover more about the problem than what was asked. |
|
Communicated the problem and solution in multiple ways |
|
Reflected on your mindset and how it help or hindered your progress. |
Problem Solving Attitude Inventory
When you are given a math problems to solve, which of the following best describes your thoughts?
Mark yes or no depending on how the statement describes you.
There are no right or wrong answers.
1. I will put down any answer just to finish a problem. Yes - No
2. It is no fun to try to solve problems. Yes - No
3. I will try almost any problem. Yes - No
4. When I do not get the right answer right away I give up. Yes - No
5. I like to try hard problems. Yes - No
6. My ideas, for solving problems, are not as good as others. Yes - No
7. I can only do problems everyone else can do. Yes - No
8. I will not stop working on a problem until I get an answer. Yes - No
9. I am sure I can solve most problems. Yes - No
10. I will work a long time on a problem. Yes - No
11. I am better than many people at solving problems. Yes - No
12. I need someone to help me work on problems. Yes - No
13. I can solve most hard problems. Yes - No
14. There are some problems I will just not try. Yes - No
15. I do not like to try problems that are hard to understand. Yes - No
16. I like to keep working on a problem until I get it right. Yes - No
17. I like to try to solve problems. Yes - No
18. I give up on problems right away. Yes - No
19. Most problems are too hard for me to solve. Yes - No
20. I am a good problem solver. Yes - No
Problems to reflect on their quality
Directions - Reflect on the similarities and differences of the following problems and their format.
- A candy maker wants to sell candies by the box. She thinks that 12 candies in a box would be a good way to sell them. How many different ways could the candies be packaged and what do you believe would be the best?
- Juan has twelve cookies and shares them with three friends, how many cookies could each have if they are to all end up with the same amount?
- Twelve divided by four is?
- 12 / 4
- 12 ÷ 4
- 4|12
- How many four foot pieces of ribbon can be cut from a twelve foot roll of ribbon?
- How many four foot square pieces of drywall can be cut from a sheet four foot by twelve foot?
- If Marci can carry four boxes at a time, how many trips will she have to make to move twelve boxes?
Mind boggler:
Think about how the format and presentation of problems on a standardized test and in a textbook limit or enhance teachers' freedom and flexibility in teaching mathematics and the learner's opportunity to become mathematically literate?
What about it?